Question

【题目】已知曲线x2+y=8与x轴交于A，B两点，动点P与A，B连线的斜率之积为 ．
（1）求动点P的轨迹C的方程．
（2）MN是动点P轨迹C的一条弦，且直线OM，ON的斜率之积为 ．求 的最小值．

Answer 1

【答案】
（1）解：在方程x2+y=8中令y=0得：x=±2 ，

∴A（﹣2 ，0），B（2 ，0）．

设P（x，y），则kAPkBP= ，整理得： ，

动点P的轨迹C的方程为

（2）解：设直线MN的方程为y=kx+m，M（x1，y1），N（x2，y2），

联立 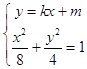，得（1+2k2）x2+4kmx+2m2﹣8=0，

∴x1+x2=﹣ ，x1x2= ，

y1y2=（kx1+m）（kx2+m）=k2 +km +m2= ，

∵kOMkON=﹣ ，∴ ，即 ，

得m2=4k2+2，

∴ =x1x2+y1y2= ，

∴﹣2≤ ＜2，

故 的最小值为﹣2

【解析】（1）由已知曲线方程求出A，B的坐标，设P（x，y），结合kAPkBP= 列式求得动点P的轨迹C的方程；（2）设直线MN的方程为y=kx+m，M（x1 ， y1），N（x2 ， y2），联立直线方程与椭圆方程，由根与系数的关系结合直线OM，ON的斜率之积为 可得m与k的关系，进一步求出 的范围得答案．