题目内容
 如图是某直三棱柱ABC-DPQ被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱ABC-DPQ被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.(1)求证:EM∥平面ABC;
(2)求出该几何体的体积.
分析:(1)取BC中点N,连接EM,AN,MN,证明四边形EMNA为平行四边形,得EM∥AN,由线面平行的判定定理,可得EM∥平面ABC.
(2)连接AD,把几何体分割成两个三棱锥,即可求解.
(2)连接AD,把几何体分割成两个三棱锥,即可求解.
解答:(1)证明:如图,取BC的中点N,连接EM,MN,AN
则MN∥CD,且MN=
CD=2
∴AE∥MN,且AE=MN
∴四边形EMNA为平行四边形
∴EM∥AN
∵EM?平面ABC,AN?平面ABC
∴EM∥平面ABC
(2) 如图,连接AD,则VVABCED=VD-ABC+VD-ABE
如图,连接AD,则VVABCED=VD-ABC+VD-ABE
由已知可知CD⊥面ABC,△ABC是等腰直角三角形,AB⊥AC,CD∥平面ABE,点D到面ABE的距离等于点C到面ABE的距离,即等于CA的长2.
∴VD-ABC=
×(
AB×AC)×DC=
×(
×2×2)×4=
VD-ABE=
×(
×AE×AB)×CA=
×(
×2×2)×2=
∴VABCED=
+
=4
故几何体的体积为4.

则MN∥CD,且MN=
| 1 |
| 2 |
∴AE∥MN,且AE=MN
∴四边形EMNA为平行四边形
∴EM∥AN
∵EM?平面ABC,AN?平面ABC
∴EM∥平面ABC
(2)
 如图,连接AD,则VVABCED=VD-ABC+VD-ABE
如图,连接AD,则VVABCED=VD-ABC+VD-ABE由已知可知CD⊥面ABC,△ABC是等腰直角三角形,AB⊥AC,CD∥平面ABE,点D到面ABE的距离等于点C到面ABE的距离,即等于CA的长2.
∴VD-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
VD-ABE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
∴VABCED=
| 8 |
| 3 |
| 4 |
| 3 |
故几何体的体积为4.
点评:本题主要考查了直线与平面平行的判定、三视图的有关知识、几何体的分割、三棱锥体积的计算.在解题中把不熟悉的几何体分割成常见几何体,体现数学解题中的化归的思想.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
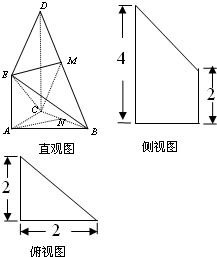 (2012•烟台三模)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(2012•烟台三模)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.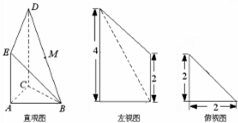 (2012•上饶一模)如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(2012•上饶一模)如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示. 如图是某直三棱柱ABC-DPQ被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱ABC-DPQ被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.