题目内容
在平面直角坐标系
中，已知圆心在
轴上，半径为4的圆
位于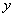
轴右侧，且与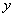轴相切．
（1）求圆
的方程；
（2）若椭圆
的离心率为
，且左右焦点为
．试探究在圆上是否存在点
，使得
为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）．
解：（1）依题意，设圆的方程为
．
∵圆与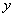轴相切，∴
∴圆的方程为
（2）∵椭圆
的离心率为
∴
解得
∴
∴
即
恰为圆心
（i）过
作
轴的垂线，交圆
，则
，符合题意；
（ii）过
可作圆的两条切线，分别与圆相切于点
，
连接
，则
，符合题意．
综上，圆上存在4个点
，使得为直角三角形．
练习册系列答案
相关题目
是边长为2的等边三角形，已知向量
满足
，
，则下列结论中正确的是 。（写出所有正确结论的序号）
为单位向量；②
为单位向量；③
；④
；⑤
，其中
成等比数列，且直线经过抛物线
的焦点，则
（ ）
B．0 C．1 D．4
中，
，
，
的对边分别为
，
，
，若
，
，
，则
___ ______．
的定义域是（）
，则a+b的值是（）
的值为（ ）
满足
，则下面结论正确是 （ ）
B．
C．
D．