题目内容
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线 的参数方程为:
的参数方程为:
 (t为参数),曲线C的极坐标方程为:
(t为参数),曲线C的极坐标方程为: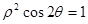 .
.
(1)求曲线C的普通方程;
(2)求直线 被曲线C截得的弦长.
被曲线C截得的弦长.
(1)  (2)
(2)
解析试题分析:解:(1)由曲线
得 化成普通方程
化成普通方程 ① 5分
① 5分
(2)方法一:把直线参数方程化为标准参数方程 (
( 为参数) ②
为参数) ②
把②代入①得:
整理,得
设其两根为 ,
,
则 8分
8分
从而弦长为 10分
10分
考点:参数方程,极坐标方程与直线与圆的位置关系
点评:解决该试题的关键是将参数方程和极坐标方程化为普通方程, 结合直线与圆的位置关系来求解,属于基础题。

练习册系列答案
相关题目
为了解800名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为( ).
| A.50 | B.40 | C.25 | D.20 |
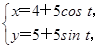 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ. 直线
直线 与曲线
与曲线
 ,
,
 中,曲线
中,曲线 的参数方程为
的参数方程为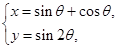 (
(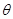 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线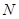 的极坐标方程为
的极坐标方程为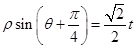 (其中
(其中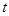 为常数).
为常数).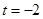 时,求曲线
时,求曲线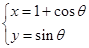 (
(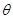 为参数),P是圆C与x轴的正半轴的交点.
为参数),P是圆C与x轴的正半轴的交点.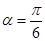 .
.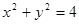 相交于两点A,B,求点P到A,B两点的距离之积.
相交于两点A,B,求点P到A,B两点的距离之积.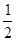 ,1),倾斜角
,1),倾斜角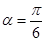 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为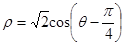 。
。