题目内容
已知椭圆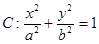 经过点(0,
经过点(0,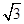 ),离心率为
),离心率为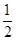 ,直线l经过椭圆C的右焦点F交
,直线l经过椭圆C的右焦点F交 椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且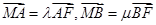 ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求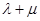 的值是否为定值?若是,求出
的值是否为定值?若是,求出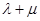 的值,否则,说明理由;
的值,否则,说明理由;
(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.

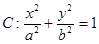 经过点(0,
经过点(0,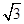 ),离心率为
),离心率为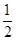 ,直线l经过椭圆C的右焦点F交
,直线l经过椭圆C的右焦点F交 椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且
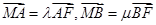 ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求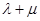 的值是否为定值?若是,求出
的值是否为定值?若是,求出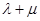 的值,否则,说明理由;
的值,否则,说明理由;(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.

(Ⅰ)依题意得b=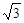 ,
,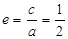 ,
,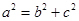 ,∴ a=2,c=1,
,∴ a=2,c=1,
∴ 椭圆C的方程 .………………3分
.………………3分
(Ⅱ)因直线l与y轴相交,故斜率存在,设直线l方程为: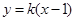 ,求得l与y轴交于M(0,-k),又F坐标为 (1,0),设l交椭圆于
,求得l与y轴交于M(0,-k),又F坐标为 (1,0),设l交椭圆于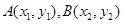 ,
,
由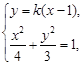 消去y得
消去y得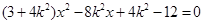 ,
,
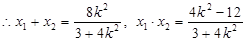 ,………5分
,………5分
又由 ∴
∴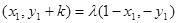 ,
,
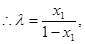 同理
同理 ,
, 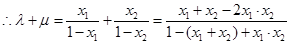 ,
,
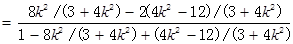
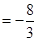 …………………7分
…………………7分
所以当直线l的倾斜角变化时,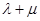 的值为定值
的值为定值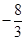 .………………8分
.………………8分
(Ⅲ)当直线l斜率不存在时,直线l⊥x轴,则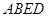 为矩形,由对称性知,AE与BD相交于FK的中点
为矩形,由对称性知,AE与BD相交于FK的中点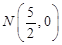 ,猜想,当直线l的倾斜角变化时,AE与BD相交于定
,猜想,当直线l的倾斜角变化时,AE与BD相交于定 点
点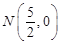 ,
,
证明:由(Ⅱ)知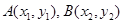 ,
, ,
,
当直线l的倾斜角变化时,首先证直线AE过定点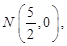
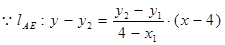 ,
,
当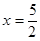 时,
时,
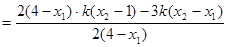
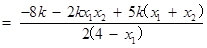
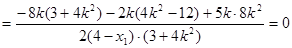 . …………………11分
. …………………11分
∴点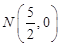 在直线
在直线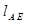 上,同理可证,点
上,同理可证,点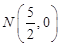 也在直线
也在直线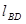 上;
上;
∴当m变化时,AE与BD相交于定点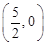 ,
,
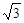 ,
,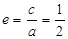 ,
,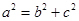 ,∴ a=2,c=1,
,∴ a=2,c=1,∴ 椭圆C的方程
 .………………3分
.………………3分(Ⅱ)因直线l与y轴相交,故斜率存在,设直线l方程为:
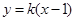 ,求得l与y轴交于M(0,-k),又F坐标为 (1,0),设l交椭圆于
,求得l与y轴交于M(0,-k),又F坐标为 (1,0),设l交椭圆于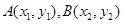 ,
,由
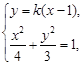 消去y得
消去y得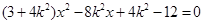 ,
,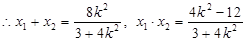 ,………5分
,………5分又由
 ∴
∴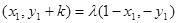 ,
,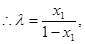 同理
同理 ,
, 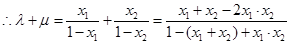 ,
,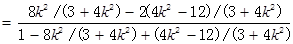
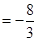 …………………7分
…………………7分所以当直线l的倾斜角变化时,
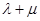 的值为定值
的值为定值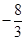 .………………8分
.………………8分(Ⅲ)当直线l斜率不存在时,直线l⊥x轴,则
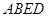 为矩形,由对称性知,AE与BD相交于FK的中点
为矩形,由对称性知,AE与BD相交于FK的中点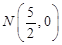 ,猜想,当直线l的倾斜角变化时,AE与BD相交于定
,猜想,当直线l的倾斜角变化时,AE与BD相交于定 点
点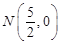 ,
,证明:由(Ⅱ)知
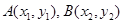 ,
, ,
,当直线l的倾斜角变化时,首先证直线AE过定点
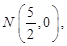
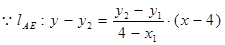 ,
,当
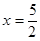 时,
时,
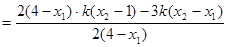
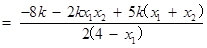
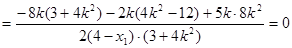 . …………………11分
. …………………11分∴点
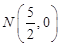 在直线
在直线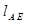 上,同理可证,点
上,同理可证,点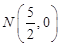 也在直线
也在直线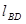 上;
上;∴当m变化时,AE与BD相交于定点
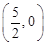 ,
, 略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
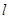 过点(0,1)并且与曲线D交于P、N两点,若O为坐标原点,满足OP⊥ON,求直线
过点(0,1)并且与曲线D交于P、N两点,若O为坐标原点,满足OP⊥ON,求直线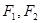 距离的和等于定长的点的轨迹是椭圆;
距离的和等于定长的点的轨迹是椭圆;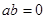 ,则
,则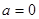 或
或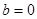 ”的逆否命题是“若
”的逆否命题是“若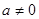 且
且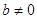 ,则ab≠0”;
,则ab≠0”;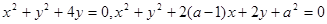 在交点处的切线互相垂直,那么实数
在交点处的切线互相垂直,那么实数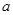 的值为
的值为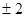 .
. 与双曲线
与双曲线 有相同的焦点,则
有相同的焦点,则 的值是
的值是
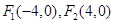 又
又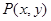 是曲线
是曲线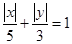 上的点,则( )
上的点,则( )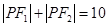
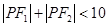
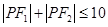
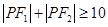
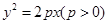 的焦点,斜率为
的焦点,斜率为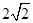 的直线交抛物线于
的直线交抛物线于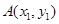 ,
,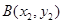
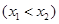 两点,且
两点,且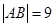 .
.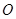 为坐标原点,是否存在平行于
为坐标原点,是否存在平行于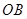 的直线
的直线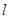 ,使得直线
,使得直线 直线
直线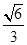 ?若存在,求出直线
?若存在,求出直线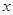 轴上的抛物线被直线
轴上的抛物线被直线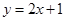 截得的弦长为
截得的弦长为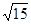 ,(1)求抛物线的方程;(2)若抛物线与直线
,(1)求抛物线的方程;(2)若抛物线与直线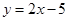 无公共点,试在抛物线上求一点,使这点到直线
无公共点,试在抛物线上求一点,使这点到直线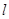 过抛物线
过抛物线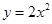 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于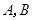 两点,则
两点,则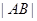 的最小值为
的最小值为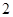 ;②双曲线
;②双曲线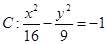 的离心率为
的离心率为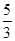 ;③若
;③若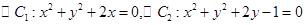 ,则这两圆恰有
,则这两圆恰有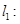
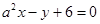 与直线
与直线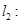
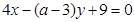 互相垂直,则
互相垂直,则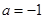 .
.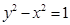 与曲线
与曲线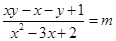 有唯一的公共点,则实数m的取值集合中元素的个数为( )
有唯一的公共点,则实数m的取值集合中元素的个数为( )