Question

（09年江苏百校样本分析）(16分)已知函数.

   (Ⅰ)当时，判断函数的单调性并写出其单调区间；

   (Ⅱ)若函数的图象与直线至少有一个交点，求实数的取值范围；

  （Ⅲ）证明对任意的，都有 成立.

Answer 1

解析：(1)当时，，其定义域为，

 ，

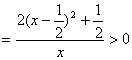∴函数为增函数，单调增区间为，         ………………………2分

   (2) 设，由题意得方程在区间上至少有一解

       ，

         令 得,    　　……………………… 4分

       ① 当时，由得，  由得或

         ∴的单调增区间为，减区间为，

         ∴，∴方程=0无解，　 

       ② 当时，，同上可得方程=0无解　  ……………… 7分

       ③ 当时，可得的单调增区间为，，单调减区间为，

         ∴极大值为 ，∴极小值，

又，

∴方程=0恰好有一解　　　　    …………………… 9分

④ 当时，≥，∴函数为增函数，由上③得方程=0也恰好有一解

⑤ 当时，的单调增区间为，减区间为，同上可得方程=0在上至少有一解                

总上得所求的取值范围为        …………………………………… 11分

   (3) 法一：由(2)可知得：当，函数在上单调增，

∴ ，即 ，…………… 12分

令，，∴,           ……………… 13分

∴ …

,

∴

即　

∴  所证结论成立.                …………………… 16分

  法二： 令 ＝ ，则

  令，，

         记      ………… 12分

           则

        单调增，                     

又

         ，时，

 即＞0

  增                      ………… 14分

又

        

 ∴  所证结论成立.                …………………… 16分