题目内容
已知数列{an}中,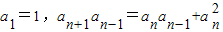 (n∈N+,n≥2),且
(n∈N+,n≥2),且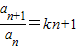 ,
,(1)求证:k=1;
(2)求数列{an}的通项公式;
(3)求数列
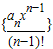 的前n项和.
的前n项和.
【答案】分析:(1)利用数列递推式,确定k+1=a2=2k,即可求得结论;
(2)利用叠乘法,可求数列{an}的通项公式;
(3)分类讨论,利用错位相减法可求数列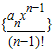 的前n项和.
的前n项和.
解答:(1)证明:∵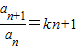 ,∴
,∴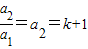 ,
,
又∵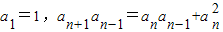 (n∈N+,n≥2)
(n∈N+,n≥2)
∴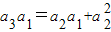 ,∴
,∴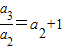 ,
,
∵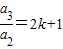 ,∴a2=2k.
,∴a2=2k.
∴k+1=a2=2k,∴k=1.
(2)解: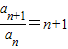 ,
,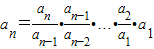 =n•(n-1)•…•2•1=n!
=n•(n-1)•…•2•1=n!
(3)解:设数列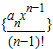 的前n项和为Sn,
的前n项和为Sn,
因为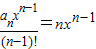 ,所以,当x=1时,
,所以,当x=1时,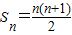 ,
,
当x≠1时,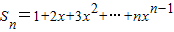 ①
①
①•x得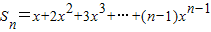 +nxn②
+nxn②
由①-②得: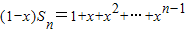 -
-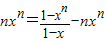
∴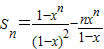
综上所述:Sn=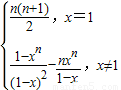
点评:本题考查数列递推式,考查叠乘法的运用,考查错位相减法求数列的和,正确运用求通项与求和的方法是关键.
(2)利用叠乘法,可求数列{an}的通项公式;
(3)分类讨论,利用错位相减法可求数列
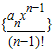 的前n项和.
的前n项和.解答:(1)证明:∵
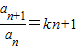 ,∴
,∴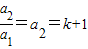 ,
,又∵
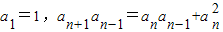 (n∈N+,n≥2)
(n∈N+,n≥2)∴
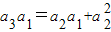 ,∴
,∴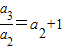 ,
,∵
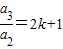 ,∴a2=2k.
,∴a2=2k.∴k+1=a2=2k,∴k=1.
(2)解:
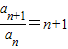 ,
,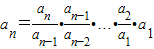 =n•(n-1)•…•2•1=n!
=n•(n-1)•…•2•1=n!(3)解:设数列
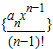 的前n项和为Sn,
的前n项和为Sn,因为
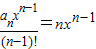 ,所以,当x=1时,
,所以,当x=1时,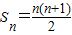 ,
,当x≠1时,
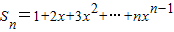 ①
①①•x得
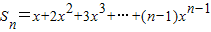 +nxn②
+nxn②由①-②得:
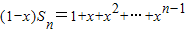 -
-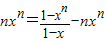
∴
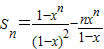
综上所述:Sn=
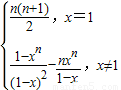
点评:本题考查数列递推式,考查叠乘法的运用,考查错位相减法求数列的和,正确运用求通项与求和的方法是关键.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|