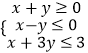��Ŀ����
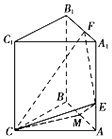
����Ŀ�����壺f1��x��=f��x������n��2��x��N*ʱ��fn��x��=f��fn��1��x���������ں���f��x���������ڵ�x0 �� ������������n��ʹ��fn��x0��=x0��������С�����������n�ǵ�x0����С�����ڣ�x0��Ϊf��x����n�����ڵ㣬��֪������[0��1]�ϵĺ���f��x����ͼ����ͼ�����ں���f��x��������˵����ȷ������д��������ȷ����ı�ţ�
��1��f��x����һ��3�����ڵ㣻
��3�ǵ� ![]() ����С�����ڣ�
����С�����ڣ�
�۶�������������n������fn�� ![]() ��=
��= ![]() ��
��
����x0�ʣ� ![]() ��1]����x0��f��x����һ��2�����ڵ㣮
��1]����x0��f��x����һ��2�����ڵ㣮
���𰸡��٢ڢ�
���������⣺f1��1��=f��1��=0��f2��1��=f��f1��1����=f��0��= ![]() ��f3��1��=f��f2��1����=f��
��f3��1��=f��f2��1����=f�� ![]() ��=1���ʢ�1��f��x����һ��3�����ڵ㣬��ȷ��
��=1���ʢ�1��f��x����һ��3�����ڵ㣬��ȷ��
f1�� ![]() ��=f��
��=f�� ![]() ��=1��f2��
��=1��f2�� ![]() ��=f��f1��
��=f��f1�� ![]() ����=f��1��=0��f3��
����=f��1��=0��f3�� ![]() ��=f��f2��
��=f��f2�� ![]() ����=f��0��=
����=f��0��= ![]() ��
��
�ʢ�3�ǵ� ![]() ����С�����ڣ���ȷ��
����С�����ڣ���ȷ��
����֪�е�ͼ��ɵã�f�� ![]() ��=
��= ![]() ��
��
��f1�� ![]() ��=f��
��=f�� ![]() ��=
��= ![]() ��f2��
��f2�� ![]() ��=f��f1��
��=f��f1�� ![]() ����=f��
����=f�� ![]() ��=
��= ![]() ��f3��
��f3�� ![]() ��=f��f2��
��=f��f2�� ![]() ����=f��
����=f�� ![]() ��=
��= ![]() ��
��
�ʢ۶�������������n������fn�� ![]() ��=
��= ![]() ����ȷ��
����ȷ��
����x0=1����x0�ʣ� ![]() ��1]����x0��f��x����һ��3�����ڵ㣬�ʴ���
��1]����x0��f��x����һ��3�����ڵ㣬�ʴ���
���Դ��ǣ��٢ڢ�
�����㾫����������Ҫ���������������ж���Ӧ�õ����֪ʶ�㣬��Ҫ�����������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ������ȷ�����⣮

����Ŀ���ڸ���ѧϰ�����У�ͬѧ�Ǿ�������˵������ѧ�������ּң���������ɼ��ã���ôѧϰ��ѧ��ûʲô���⣮��ij����ԡ�����������ѧϰ����ѧѧϰ��Ӱ�족�����о����õ����ն����������ɼ�����ѧ�ɼ�����������ع�ϵ�Ľ��ۣ��ִӸð������ȡ5��ѧ����һ�ο����е���ѧ�������ɼ��������
�ɼ� ��� | 1 | 2 | 3 | 4 | 5 |
������x�� | 90 | 85 | 74 | 68 | 63 |
��ѧ��y�� | 130 | 125 | 110 | 95 | 90 |
��1������ѧ�ɼ�y�������ɼ�x�����Իع鷽�� ![]() =
= ![]() x+
x+ ![]() ��
�� ![]() ��ȷ��0.1������ijλѧ���������ɼ�Ϊ80�֣�Ԥ��������ѧ�ɼ���
��ȷ��0.1������ijλѧ���������ɼ�Ϊ80�֣�Ԥ��������ѧ�ɼ���
��2��Ҫ�ӳ�ȡ������λѧ�������ѡ��2λ�μ�һ��֪ʶ��������ѡ�е�ѧ������ѧ�ɼ�������һλ����120�ֵĸ��ʣ����ο���ʽ�� ![]() =
=  ��
�� ![]() =
= ![]() ��
�� ![]() �� ���ο����ݣ�902+852+742+682+632=29394��90����125+74��110+68��95+63��90=42595��
�� ���ο����ݣ�902+852+742+682+632=29394��90����125+74��110+68��95+63��90=42595��