Question

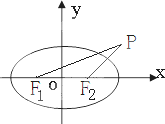已知F₁，F₂是椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的左右焦点，点P（a，b），若△F₁PF₂为等腰三角形．
（1）求椭圆的离心率；
（2）设直线PF₂与椭圆相交于A，B两点，M是直线PF₂上的动点，满足

AM

•

BM

=-2，求点M的轨迹方程．

Answer 1

分析：（1）由题意可知P在第一象限，且PF₂=F₁F₂，由两点间的距离公式求出PF₂的长度，利用PF₂=2c列式可求椭圆的离心率；
（2）由P和F₂的坐标写出PF₂的斜率，写出直线方程，和椭圆方程联立求出A点坐标，可知B得坐标，设出M的坐标后得到向量

AM

，

BM

的坐标，代入

AM

•

BM

=-2后整理可得点M的轨迹方程．

解答：解：（1）由△F₁PF₂为等腰三角形，若PF₁=PF₂，则P点在y轴上，与P（a，b）矛盾，
所以PF₂=F₁F₂，所以PF₂=2c，
由F₂（c，0），所以PF22=（a-c）²+b²=4c²，把b²=a²-c²代入得，
a²-2ac+c²+a²-c²=4c²，整理得：2c²+ac-a²=0．
即2e²+e-1=0，（2e-1）（e+1）=0，解得：e=

1

2

；
（2）直线PA为y=

b

a-c

x-

bc

a-c

，
又a=2c，所以PA方程为y=

b

c

x-b．
代入椭圆方程得A交点为（

8

5

c，

3

5

b），B为（0，-b）．
设M（x，y），
则

AM

=(x-

8

5

c，y-

3

5

b)，

BM

=(x，y+b)．
由

AM

•

BM

=-2，得
(x-

8

5

c)x+(y-

3

5

b)(y+b)=-2，
整理得
x2-

8

5

cx+y2+

2

5

by-

3

5

b2+2=0．

点评：本题考查了圆锥曲线的轨迹方程问题，考查了椭圆的简单几何性质，训练了平面向量在解题中的应用，解答此题的关键是明确P点的坐标与椭圆的长半轴和短半轴一致，此题是中档题．