Question

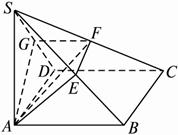
已知矩形ABCD，过A作SA⊥平面AC，再过A作AE⊥SB交SB于E，过E作EF⊥SC交SC于F

(1)求证：AF⊥SC

(2)若平面AEF交SD于G，求证：AG⊥SD

Answer 1

解析:

如图，欲证AF⊥SC，只需证SC垂直于AF所在平面，即SC⊥平面AEF，由已知，欲证SC⊥平面AEF，只需证AE垂直于SC所在平面，即AE⊥平面ABC，再由已知只需证AE⊥BC，而要证AE⊥BC，只需证BC⊥平面SAB，而这可由已知得证

证明  (1)∵SA⊥平面AC，BC平面AC，∴SA⊥BC

∵矩形ABCD，∴AB⊥BC

∴BC⊥平面SAB

∴BC⊥AE又SB⊥AE  ∴AE⊥平面SBC

∴SC⊥平面AEF

∴AF⊥SC

(2)∵SA⊥平面AC  ∴SA⊥DC，又AD⊥DC

∴DC⊥平面SAD  ∴DC⊥AG

又由(1)有SC⊥平面AEF，AG平面AEF

∴SC⊥AG  ∴AG⊥平面SDC  ∴AG⊥SD