题目内容
 在五边形ABCDE中(图一),BD是AC的垂直平分线,O为垂足.ED∥AC,AE∥BD,AB⊥BC,P为AB的中点.沿对角线AC将四边形ACDE折起,使平面ACDE⊥平面ABC(图二).
在五边形ABCDE中(图一),BD是AC的垂直平分线,O为垂足.ED∥AC,AE∥BD,AB⊥BC,P为AB的中点.沿对角线AC将四边形ACDE折起,使平面ACDE⊥平面ABC(图二). (1)求证:PE∥平面DBC;
(2)当AB=
| 2 |
分析:(1)证明四边形PMDE为平行四边形,可得EP∥DM,利用线面平行的判定定理,可得PE∥平面DBC;
(2)建立空间直角坐标系,设|AE|=2,则AB=2
,求出平面PBC的法向量,利用向量的夹角公式,即可求直线DA与平面DBC所成角的正弦值.
(2)建立空间直角坐标系,设|AE|=2,则AB=2
| 2 |
解答: (1)证明:设M为BC中点,连PM,DM 依题意,ED
(1)证明:设M为BC中点,连PM,DM 依题意,ED
AC
∵P、M分别为AB、BC的中点,∴PM
AC
∴ED
PM,…(3分)
∴四边形PMDE为平行四边形,∴EP∥DM
又DM?平面DBC,PE?平面DBC,
∴PE∥平面DBC…(5分)
(2)解:以点O为原点,直线OA、OB、OD所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,不 妨设|AE|=2,则A(2,0,0)、B(0,2,0)C(-2,0,0)、
妨设|AE|=2,则A(2,0,0)、B(0,2,0)C(-2,0,0)、
D(0,0,2)、E(2,0,2)、P(1,1,0)…(6分)
∴
=(2,0,-2)、
=(-2,-2,0)、
=(0,2,-2)…(7分)
设平面PBC的法向量为
=(x,y,z),
则由
,得
,…(9分)
令x=1,则y=z=-1,∴
=(1,-1,-1),
∴cos<
,
>=
=
,
∴直线DA与平面DBC所成角的正弦值为
.…(12分)
 (1)证明:设M为BC中点,连PM,DM 依题意,ED
(1)证明:设M为BC中点,连PM,DM 依题意,ED
| ||
. |
| 1 |
| 2 |
∵P、M分别为AB、BC的中点,∴PM
| ||
. |
| 1 |
| 2 |
∴ED
| ||
. |
∴四边形PMDE为平行四边形,∴EP∥DM
又DM?平面DBC,PE?平面DBC,
∴PE∥平面DBC…(5分)
(2)解:以点O为原点,直线OA、OB、OD所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,不
 妨设|AE|=2,则A(2,0,0)、B(0,2,0)C(-2,0,0)、
妨设|AE|=2,则A(2,0,0)、B(0,2,0)C(-2,0,0)、D(0,0,2)、E(2,0,2)、P(1,1,0)…(6分)
∴
| DA |
| BC |
| DB |
设平面PBC的法向量为
| n |
则由
|
|
令x=1,则y=z=-1,∴
| n |
∴cos<
| DA |
| n |
| ||||
|
|
| ||
| 3 |
∴直线DA与平面DBC所成角的正弦值为
| ||
| 3 |
点评:本题考查线面平行,考查线面角,考查向量知识的运用,考查学生的计算能力,确定平面的法向量是关键.

练习册系列答案
相关题目
 中,不等式
中,不等式 成立;在四边形ABCD中,不等式
成立;在四边形ABCD中,不等式 成立;在五边形ABCDE中,不等式
成立;在五边形ABCDE中,不等式 成立……,依此类推,在n边形
成立……,依此类推,在n边形 中,不等式
中,不等式 成立。
成立。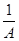 +
+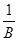 +
+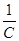 ≥
≥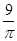 成立,在四边形ABCD中,不等式
成立,在四边形ABCD中,不等式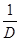 ≥
≥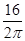 成立,在五边形ABCDE中,不等式
成立,在五边形ABCDE中,不等式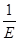 ≥
≥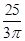 成立,猜想在n边形A1A2…An中,有不等式 (n≥3)成立.
成立,猜想在n边形A1A2…An中,有不等式 (n≥3)成立.