题目内容
已知球的表面积为20π,球面上有A、B、C三点,如果AB=AC=2,BC=
解析:求出球的半径R及过A、B、C三点的外接圆的半径r,利用d、r、R的关系即可求出d.
如图,设球的球心是O,由于O到A、B、C的距离都是球的半径R,所以O在平面ABC内的射影O′是△ABC的外心.

在△ABC中,由余弦定理得
cos∠BAC=![]() ,
,
∴∠BAC=120°.
设△ABC的外接圆的半径为r,则![]() ,
,
∴![]() =2r.∴r=2.
=2r.∴r=2.
∵S球=4πR2=20π,∴R2=5.
∴球心O到平面ABC的距离OO′=R2-r2=5-4=1.
小结:本题的解题过程是利用正弦定理、余弦定理求出△ABC的外接圆的半径r,利用球面的面积公式求出球的半径R,再利用球半径、截面圆半径及球心到截面之间的关系求出要求的距离,也可以利用等腰三角形的性质,求出底边高,再利用外接圆半径都相等,也可以利用直角三角形的勾股定理列方程求解.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
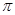 ,球面上有A、B、C三点,如果AB=AC=2,BC=2
,球面上有A、B、C三点,如果AB=AC=2,BC=2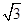 ,则球心到平面ABC的距离为( )
,则球心到平面ABC的距离为( )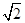 C.
C.