题目内容
已知向量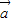 =(cos
=(cos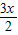 ,sin
,sin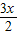 ),
),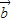 =(cos
=(cos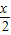 ,-sin
,-sin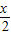 ),
),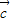 =(
=(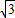 ,-1),其中x∈R.
,-1),其中x∈R.(I)当
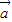 ⊥
⊥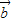 时,求x值的集合;
时,求x值的集合;(Ⅱ)求|
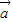 -
-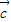 |的最大值.
|的最大值.
【答案】分析:(1)根据数量积是否为零判断两个平面向量的垂直关系,建立等量关系,求出x即可;
(2)求向量的模时一般的处理方法是先计算模的平方,即利用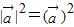 得到一个三角函数,求出其最大值即可.
得到一个三角函数,求出其最大值即可.
解答:解:(I)由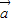 ⊥
⊥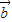 ⇒
⇒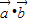 =0,(2分)
=0,(2分)
即cos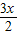 cos
cos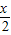 -sin
-sin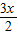 sin
sin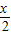 =0,得cos2x=0,(5分)
=0,得cos2x=0,(5分)
则2x=kπ+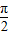 (k∈Z),∴x=
(k∈Z),∴x=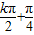 (k∈Z),
(k∈Z),
∴当 ⊥
⊥ 时,x值的集合为{x|x=
时,x值的集合为{x|x=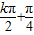 (k∈Z)};(7分)
(k∈Z)};(7分)
(Ⅱ)|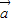 -
-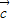 |2=(
|2=(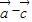 )2=
)2=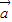 2-2
2-2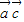 +
+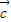 2=|
2=|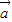 |2-2
|2-2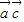 +|
+|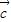 |2,(9分)
|2,(9分)
又|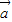 |2=(cos
|2=(cos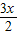 )2+(sin
)2+(sin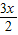 )2=1,|
)2=1,|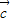 |2=(
|2=(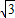 )2+(-1)2=4,
)2+(-1)2=4,
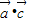 =
=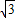 cos
cos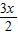 -sin
-sin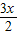 =2(
=2(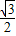 cos
cos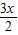 -
- sin
sin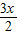 )=2cos(
)=2cos(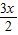 +
+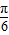 ),
),
∴|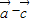 |2=1-4cos(
|2=1-4cos(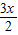 +
+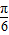 )+4=5-4cos(
)+4=5-4cos(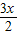 +
+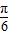 ),(13分)
),(13分)
∴|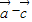 |2max=9,∴|
|2max=9,∴|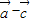 |max=3,
|max=3,
即|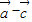 |的最大值为3.(15分)
|的最大值为3.(15分)
点评:本题主要考查了数量积判断两个平面向量的垂直关系,以及向量的模和两角和与差的余弦函数,属于基础题.
(2)求向量的模时一般的处理方法是先计算模的平方,即利用
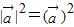 得到一个三角函数,求出其最大值即可.
得到一个三角函数,求出其最大值即可.解答:解:(I)由
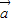 ⊥
⊥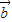 ⇒
⇒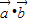 =0,(2分)
=0,(2分)即cos
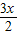 cos
cos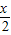 -sin
-sin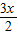 sin
sin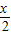 =0,得cos2x=0,(5分)
=0,得cos2x=0,(5分)则2x=kπ+
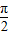 (k∈Z),∴x=
(k∈Z),∴x=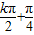 (k∈Z),
(k∈Z),∴当
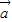 ⊥
⊥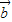 时,x值的集合为{x|x=
时,x值的集合为{x|x=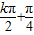 (k∈Z)};(7分)
(k∈Z)};(7分)(Ⅱ)|
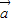 -
-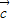 |2=(
|2=(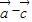 )2=
)2=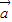 2-2
2-2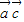 +
+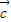 2=|
2=|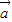 |2-2
|2-2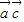 +|
+|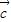 |2,(9分)
|2,(9分)又|
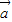 |2=(cos
|2=(cos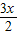 )2+(sin
)2+(sin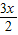 )2=1,|
)2=1,|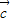 |2=(
|2=(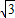 )2+(-1)2=4,
)2+(-1)2=4,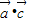 =
=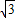 cos
cos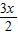 -sin
-sin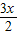 =2(
=2(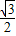 cos
cos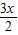 -
- sin
sin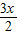 )=2cos(
)=2cos(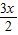 +
+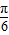 ),
),∴|
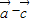 |2=1-4cos(
|2=1-4cos(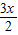 +
+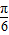 )+4=5-4cos(
)+4=5-4cos(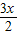 +
+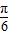 ),(13分)
),(13分)∴|
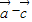 |2max=9,∴|
|2max=9,∴|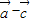 |max=3,
|max=3,即|
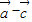 |的最大值为3.(15分)
|的最大值为3.(15分)点评:本题主要考查了数量积判断两个平面向量的垂直关系,以及向量的模和两角和与差的余弦函数,属于基础题.

练习册系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |