题目内容
已知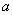 为正实数,
为正实数,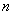 为自然数,抛物线
为自然数,抛物线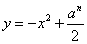 与
与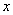 轴正半轴相交于点
轴正半轴相交于点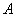 .设
.设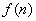 为该抛物线在点
为该抛物线在点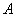 处的切线在
处的切线在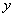 轴上的截距.
轴上的截距.
⑴用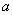 和
和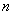 表示
表示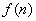 ;
;
⑵求对所有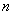 都有
都有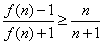 成立的
成立的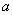 的最小值;
的最小值;
⑶当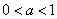 时,比较
时,比较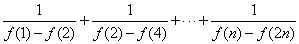 与
与
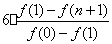 的大小,并说明理由.
的大小,并说明理由.
【解析】⑴由已知得,交点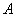 的坐标为
的坐标为 ,对
,对 求导得
求导得 ,
,
则抛物线在点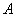 处的切
处的切 线方程为
线方程为 ,即
,即 ,则
,则 .
.
⑵由⑴知 ,则
,则 成立的充要条
成立的充要条 件是
件是 .
.
即 对所有的
对所有的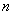 都成立.特别地,取
都成立.特别地,取 得到
得到 .
.
当 ,
, 时,
时, .当
.当 时,
时, .
.
故 时,
时,  对所有自然数
对所有自然数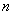 均成立.所以满足条件的
均成立.所以满足条件的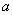 的最小值为
的最小值为 .
.
⑶由⑴知 .
.
下面证明: .
.
首先证明:当 时,
时, .
.
设函数 ,
, ,则
,则 .
.
当 时,
时, ;当
;当 时,
时, .
.
故 在区间
在区间 的最小值
的最小值 .
.
所以,当 时,
时,  ,即得
,即得 .
.
由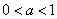 知
知
 ,因此
,因此 ,从而
,从而

 .
.

练习册系列答案
相关题目
 表示的平面区域内运动,则z=x-y的取值范围是( )
表示的平面区域内运动,则z=x-y的取值范围是( ) 上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题
上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题 D.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+
D.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+ 1≥0”
1≥0” 有解,则整数
有解,则整数 的值只能有( )
的值只能有( )
 B.
B. C.
C.  D.
D.
 不等式
不等式 的解集是R,命题
的解集是R,命题 在区间
在区间 上是减函数,若命题“
上是减函数,若命题“ ”为真,则实数
”为真,则实数 的范围是______.
的范围是______. 与圆
与圆 相切,那么
相切,那么 的最大值为
的最大值为 C. 2 D.
C. 2 D.
 <0,那么角
<0,那么角 是( ).
是( ).