题目内容
 正四棱柱ABCD-A1B1C1D1的底面边长是
正四棱柱ABCD-A1B1C1D1的底面边长是| 3 |
①求证:A1C⊥面AEF;
②延伸平面AEF与CC1交于点M,求平面AEF与平面ABD所成的二面角;
③求多面体ABCD-EFM的体积.
分析:①根据三垂线定理逆定理,先利用AC1在平面A1B上的射影为A1B以及A1B⊥AE得到A1C⊥AE;同理A1C⊥AF.即可证A1C⊥平面AEF;
②延长ME,CB交于点G,连AG,则AG为平面AEF与平面ABD的交线,易证得AG∥BD,连AC,连AM,则∠MAC为所求二面角的平面角.
③将多面体ABCD-EFM进行割补.过EF作面ENFH∥面ABCD,分别交AA1、CC1于H、N.则VM-EFN=VA-EFH,于是利用VABCD-EFM=VABCD-HENF求解.
②延长ME,CB交于点G,连AG,则AG为平面AEF与平面ABD的交线,易证得AG∥BD,连AC,连AM,则∠MAC为所求二面角的平面角.
③将多面体ABCD-EFM进行割补.过EF作面ENFH∥面ABCD,分别交AA1、CC1于H、N.则VM-EFN=VA-EFH,于是利用VABCD-EFM=VABCD-HENF求解.
解答: 解:①证明:∵CB⊥平面A1B,
解:①证明:∵CB⊥平面A1B,
∴AC1在平面A1B上的射影为A1B.
又A1B⊥AE,AE?平面A1B,
由三垂线定理逆定理,
∴A1C⊥AE.同理A1C⊥AF,
∵AE∩AF=A,
∴A1C⊥平面AEF.
(2)延长ME,CB交于点G,连AG,则AG为平面AEF与平面ABD的交线.
由题可得
,所以△A1AB∽△ABE,
=
,BE=
=
=1,同理求得DF=1.
∴BE=FD,又∵BE∥FD,∴四边形BEFD为平行四边形,∴EF∥BD.
∵EF?平面ABD,BD?平面ABD,根据直线和平面平行的判定定理,得出EF∥平面ABD,∵EF?平面AEF,平面AEF∩平面ABD=AG,利用直线和平面平行的判定定理得出EF∥AG.∴AG∥BD,且B为GC中点.
连接AC,连AM,由BD⊥AC,BD⊥AM,得出AG⊥AC,AG⊥AM,所以∠MAC为所求二面角的平面角.
在RT△MAC中,MC=2BE=2,AC=
•
=
,tan∠MAC=
=
=
,
∴∠MAC=arctan
.
(3)过EF作面ENFH∥面ABCD,分别交AA1、CC1于H、N
则VM-EFN=VA-EFH∴VABCD-EFM=VABCD-HENF=3×2=6.
 解:①证明:∵CB⊥平面A1B,
解:①证明:∵CB⊥平面A1B,∴AC1在平面A1B上的射影为A1B.
又A1B⊥AE,AE?平面A1B,
由三垂线定理逆定理,
∴A1C⊥AE.同理A1C⊥AF,
∵AE∩AF=A,
∴A1C⊥平面AEF.
(2)延长ME,CB交于点G,连AG,则AG为平面AEF与平面ABD的交线.
由题可得
|
| A1A |
| AB |
| AB |
| BE |
| AB2 |
| A1A |
(
| ||
| 3 |
∴BE=FD,又∵BE∥FD,∴四边形BEFD为平行四边形,∴EF∥BD.
∵EF?平面ABD,BD?平面ABD,根据直线和平面平行的判定定理,得出EF∥平面ABD,∵EF?平面AEF,平面AEF∩平面ABD=AG,利用直线和平面平行的判定定理得出EF∥AG.∴AG∥BD,且B为GC中点.
连接AC,连AM,由BD⊥AC,BD⊥AM,得出AG⊥AC,AG⊥AM,所以∠MAC为所求二面角的平面角.
在RT△MAC中,MC=2BE=2,AC=
| 2 |
| 3 |
| 6 |
| MC |
| AC |
| 2 | ||
|
| ||
| 3 |
∴∠MAC=arctan
| ||
| 3 |
(3)过EF作面ENFH∥面ABCD,分别交AA1、CC1于H、N
则VM-EFN=VA-EFH∴VABCD-EFM=VABCD-HENF=3×2=6.
点评:本题综合考查了直线和平面垂直的判定和性质以及无棱二面角求解,不规则几何体体积计算.考查空间想象能力、推理论证能力运算求解能力.无棱二面角求解一般要进行平面延展,得出棱.

练习册系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
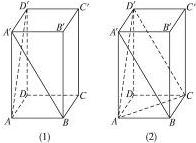 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是