题目内容
关于函数f(x)=4sin(2x+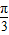 )(x∈R)有下列命题,
)(x∈R)有下列命题,①y=f(x)图象关于直线x=-
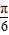 对称
对称 ②y=f(x)的表达式可改写为y=4cos(2x-
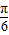 )
)③y=f(x)的图象关于点(-
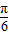 ,0)对称
,0)对称 ④由f(x1)=f(x2)=0可得x1-x2必是π的整数倍.
其中正确命题的序号是 .
【答案】分析:①由f(x)=4sin(2x+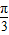 )(x∈R),知y=f(x)图象的对称轴方程满足2x+
)(x∈R),知y=f(x)图象的对称轴方程满足2x+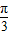 =kπ+
=kπ+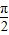 ,k∈Z,由此能求出y=f(x)图象的对称轴;
,k∈Z,由此能求出y=f(x)图象的对称轴;
②由f(x)=4sin(2x+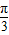 )(x∈R),利用诱导公式能推导出y=f(x)=4cos(
)(x∈R),利用诱导公式能推导出y=f(x)=4cos(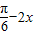 )=4cos(2x-
)=4cos(2x-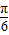 );
);
③由f(x)=4sin(2x+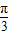 )(x∈R)的对称点是(
)(x∈R)的对称点是(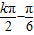 ,0),能求出y=f(x)的图象关于点(-
,0),能求出y=f(x)的图象关于点(-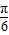 ,0)对称;
,0)对称;
④由f(x1)=f(x2)=0可得x1-x2必是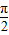 π的整数倍.
π的整数倍.
解答:解:∵f(x)=4sin(2x+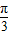 )(x∈R),
)(x∈R),
∴y=f(x)图象的对称轴方程满足2x+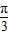 =kπ+
=kπ+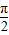 ,k∈Z,
,k∈Z,
即y=f(x)图象关于直线x=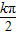 +
+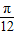 ,k∈Z对称,故①不正确;
,k∈Z对称,故①不正确;
∵f(x)=4sin(2x+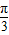 )(x∈R),
)(x∈R),
∴y=f(x)=4cos[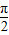 -(2x+
-(2x+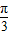 )]=4cos(
)]=4cos(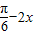 )=4cos(2x-
)=4cos(2x-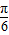 ),故②正确;
),故②正确;
∵f(x)=4sin(2x+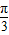 )(x∈R)的对称点是(
)(x∈R)的对称点是(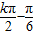 ,0),
,0),
∴y=f(x)的图象关于点(-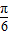 ,0)对称,故③正确;
,0)对称,故③正确;
由f(x1)=f(x2)=0可得x1-x2必是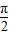 π的整数倍,故④不正确.
π的整数倍,故④不正确.
故答案为:②③.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答,注意三角函数性质的合理运用.
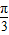 )(x∈R),知y=f(x)图象的对称轴方程满足2x+
)(x∈R),知y=f(x)图象的对称轴方程满足2x+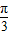 =kπ+
=kπ+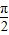 ,k∈Z,由此能求出y=f(x)图象的对称轴;
,k∈Z,由此能求出y=f(x)图象的对称轴;②由f(x)=4sin(2x+
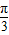 )(x∈R),利用诱导公式能推导出y=f(x)=4cos(
)(x∈R),利用诱导公式能推导出y=f(x)=4cos(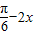 )=4cos(2x-
)=4cos(2x-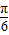 );
);③由f(x)=4sin(2x+
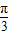 )(x∈R)的对称点是(
)(x∈R)的对称点是(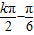 ,0),能求出y=f(x)的图象关于点(-
,0),能求出y=f(x)的图象关于点(-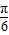 ,0)对称;
,0)对称;④由f(x1)=f(x2)=0可得x1-x2必是
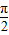 π的整数倍.
π的整数倍.解答:解:∵f(x)=4sin(2x+
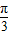 )(x∈R),
)(x∈R),∴y=f(x)图象的对称轴方程满足2x+
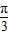 =kπ+
=kπ+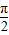 ,k∈Z,
,k∈Z,即y=f(x)图象关于直线x=
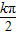 +
+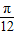 ,k∈Z对称,故①不正确;
,k∈Z对称,故①不正确;∵f(x)=4sin(2x+
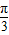 )(x∈R),
)(x∈R),∴y=f(x)=4cos[
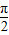 -(2x+
-(2x+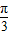 )]=4cos(
)]=4cos(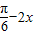 )=4cos(2x-
)=4cos(2x-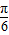 ),故②正确;
),故②正确;∵f(x)=4sin(2x+
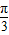 )(x∈R)的对称点是(
)(x∈R)的对称点是(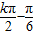 ,0),
,0),∴y=f(x)的图象关于点(-
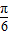 ,0)对称,故③正确;
,0)对称,故③正确;由f(x1)=f(x2)=0可得x1-x2必是
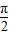 π的整数倍,故④不正确.
π的整数倍,故④不正确.故答案为:②③.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答,注意三角函数性质的合理运用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 )(
)( ),有下列命题:
),有下列命题: 可得
可得 必是
必是 的整数倍;
的整数倍;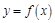 的表达式可改写为
的表达式可改写为 ;
; 对称;
对称; 对称.
对称.