题目内容
在平面直角坐标系中,已知点P(1,-1),过点P作抛物线T0:y=x2的切线,其切点分别为M(x1,y1),N(x2,y2)(其中x1<x2)。
(1)求x1与x2的值;
(2)若以点P为圆心的圆E与直线MN相切,求圆E的方程;
(3)过原点O(0,0)作圆E的两条互相垂直的弦AC,BD,求四边形ABCD面积的最大值。
(1)求x1与x2的值;
(2)若以点P为圆心的圆E与直线MN相切,求圆E的方程;
(3)过原点O(0,0)作圆E的两条互相垂直的弦AC,BD,求四边形ABCD面积的最大值。
解:(1)由y=x2可得y'=2x
∵直线PM与曲线T0相切,且过点P(1,-1),
∴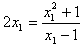 ,即
,即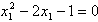
∴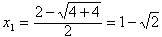 或
或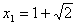
同理可得: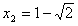 或
或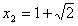
∵x1<x2,
∴x1=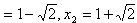 。
。
(2)由(1),可知x1+x2=2,x1·x2=-1,
则直线MN的斜率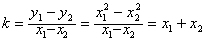
∴直线M的方程为:y-y1=(x1+x2)(x-x1),
又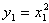 ,
,
∴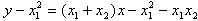
即2x-y+1=0
∵点P到直线MN的距离即为圆E的半径,
即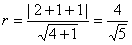
故圆E的方程为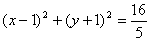 。
。
(3)四边形ABCD的面积为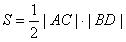
不妨设圆心E到直线AC的距离为d1,垂足为E1;
圆心E到直线BD的距离为d2,垂足为E2;
则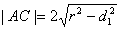 ,
,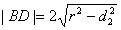
由于四边形EE1OE2为矩形,且
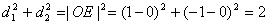
所以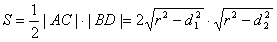
由基本不等式2ab≤a2+b2可得
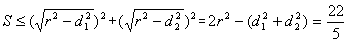
当且仅当d1=d2时等号成立。
∵直线PM与曲线T0相切,且过点P(1,-1),
∴
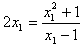 ,即
,即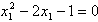
∴
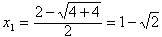 或
或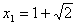
同理可得:
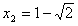 或
或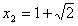
∵x1<x2,
∴x1=
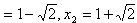 。
。(2)由(1),可知x1+x2=2,x1·x2=-1,
则直线MN的斜率
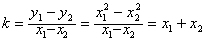
∴直线M的方程为:y-y1=(x1+x2)(x-x1),
又
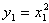 ,
,∴
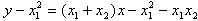
即2x-y+1=0
∵点P到直线MN的距离即为圆E的半径,
即
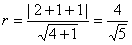
故圆E的方程为
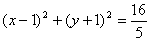 。
。(3)四边形ABCD的面积为
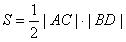
不妨设圆心E到直线AC的距离为d1,垂足为E1;
圆心E到直线BD的距离为d2,垂足为E2;
则
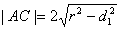 ,
,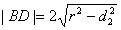
由于四边形EE1OE2为矩形,且
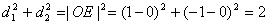
所以
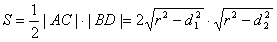
由基本不等式2ab≤a2+b2可得
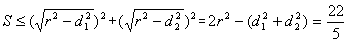
当且仅当d1=d2时等号成立。

练习册系列答案
相关题目