题目内容
若函数y=f（x）是一次函数，且有f[f（x）]=4x-3，求函数y=f（x）的解析式．
解：∵函数y=f（x）是一次函数，
∴设f（x）=ax+b（a≠0），
所以f[f（x）]=a（ax+b）+b=a2x+ab+b，
又∵f[f（x）]=4x-3，
∴
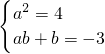，解得
，
∴f（x）=2x-1或f（x）=-2x+3．
分析：根据题意可设f（x）=ax+b（a≠0），所以f[f（x）]=a（ax+b）+b=a2x+ab+b，结合f[f（x）]=4x-3可得a与b的数值，进而得到答案．
点评：本题主要考查求解析式的方法以及一次函数的特征．
∴设f（x）=ax+b（a≠0），
所以f[f（x）]=a（ax+b）+b=a2x+ab+b，
又∵f[f（x）]=4x-3，
∴
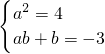，解得，∴f（x）=2x-1或f（x）=-2x+3．
分析：根据题意可设f（x）=ax+b（a≠0），所以f[f（x）]=a（ax+b）+b=a2x+ab+b，结合f[f（x）]=4x-3可得a与b的数值，进而得到答案．
点评：本题主要考查求解析式的方法以及一次函数的特征．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目