题目内容
在下列命题中：①若向量
共线，则向量所在直线平行 ②若三个向量
两两共面，则共面；③已知空间的三个向量，则对空间的任意一个向量
总存在实数
使得
。其中正确的命题个数是（ ）
| A．0 | B．1 | C．2 | D．3 |
A
解析试题分析：对于命题①若向量共线，则向量所在直线平行或重合，不正确；对于命题②举反例：当向量所在直线为棱锥顶点引出的三条棱，则不共面，不正确；对于命题③当空间向量共面时，就满足不了题目中的结论，不正确。故正确的命题个数为0个，故选A∵，∴
考点：本题主要考查了向量共线定义、共面基本定理及空间向量基本定理。
点评：掌握向量共线、共面及空间基本定理是解决关键。
练习册系列答案
相关题目
下列有关命题的说法正确的是 ( )
A．命题“若 ，则 ”的否命题为：“若，则 ”． |
B．“ ”是“ ”的必要不充分条件． |
C．命题“ 使得 ”的否定是：“ 均有”． |
D．命题“若 ，则 ”的逆否命题为真命题． |
下列命题中，是真命题的是（ ）
A． | B． |
C． | D． |
“
”是“直线
与直线
平行”的（ ）
| A．充分必要条件 | B．充分而不必要条件 |
| C．必要而不充分条件 | D．既不充分也不必要条件 |
已知命题p：
，则
为（ ）。
A． , | B． , |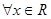
C．, | D．：， |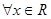
已知P：|2x－3|<1, Q：x(x－3)<0, 则P是Q的（ ）
| A．充分不必要条件； | B．必要不充分条件 ； |
| C．充要条件 ； | D．既不充分也不必要条件 |
若命题p：
，则┑p 为（ ）
A． | B． |
C． | D． |
;
是
的充分不必要条件