题目内容
已知数列{an}中,a1=1,a2=0,对任意正整数n,m(n>m)满足 ,则a119=________.
,则a119=________.
-1
分析:令n=2,m=1,则(a2)2-(a1)2=a1a3;因为a1=1,a2=0,所以a3=-1,令n>2,m=2,则(an)2-(a2)2=an-2an+2,所以 由此可求a119的值.
由此可求a119的值.
解答:令n=2,m=1,则(a2)2-(a1)2=a1a3;
因为a1=1,a2=0,所以a3=-1;
令n>2,m=2,则(an)2-(a2)2=an-2an+2,
所以 ;
;
所以 =…=
=…=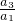 =-1
=-1
所以 =-1;
=-1;
所以a119=-a1=-1
点评:本题考查归纳推理,考查赋值法的运用,解题的关键是正确赋值,属于基础题.
分析:令n=2,m=1,则(a2)2-(a1)2=a1a3;因为a1=1,a2=0,所以a3=-1,令n>2,m=2,则(an)2-(a2)2=an-2an+2,所以
 由此可求a119的值.
由此可求a119的值.解答:令n=2,m=1,则(a2)2-(a1)2=a1a3;
因为a1=1,a2=0,所以a3=-1;
令n>2,m=2,则(an)2-(a2)2=an-2an+2,
所以
 ;
;所以
 =…=
=…=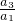 =-1
=-1所以
 =-1;
=-1;所以a119=-a1=-1
点评:本题考查归纳推理,考查赋值法的运用,解题的关键是正确赋值,属于基础题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|