题目内容
以下四个关于圆锥曲线的命题中:①设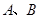 为两个定点,
为两个定点,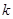 为非零常数,
为非零常数,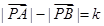 ,则动点
,则动点 的轨迹为双曲线;②过定圆
的轨迹为双曲线;②过定圆 上一定点
上一定点 作圆的动点弦
作圆的动点弦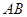 ,
, 为坐标原点,若
为坐标原点,若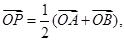 则动点
则动点 的轨迹为圆;③设
的轨迹为圆;③设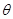 是
是 的一内角,且
的一内角,且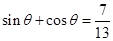 ,则
,则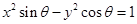 表示焦点在
表示焦点在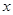 轴上的双曲线;④已知两定点
轴上的双曲线;④已知两定点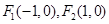 和一动点
和一动点 ,若
,若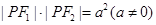 ,则点
,则点 的轨迹关于原点对称.
的轨迹关于原点对称.
其中真命题的序号为 (写出所有真命题的序号).
②④
解析试题分析:对于①,由双曲线的定义可知,动点 的轨迹为双曲线的一支,所以①不正确;对于②,由
的轨迹为双曲线的一支,所以①不正确;对于②,由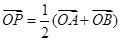 ,可知点
,可知点 为弦
为弦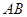 的中点,连结
的中点,连结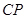 ,则有
,则有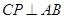 即
即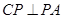 ,而
,而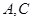 均为定点,所以
均为定点,所以 点的轨迹是以
点的轨迹是以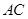 为直径的圆,所以②正确;对于③,由
为直径的圆,所以②正确;对于③,由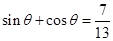 两边平方可得
两边平方可得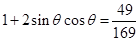 ,所以
,所以 ,因为
,因为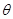 是
是 的一个内角,可判断
的一个内角,可判断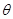 为钝角,所以
为钝角,所以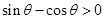 且
且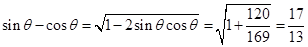 ,联立
,联立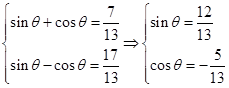 ,从而方程
,从而方程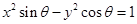 为
为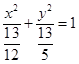 ,表示焦点在
,表示焦点在 轴上的椭圆,所以③错误;对于④,设动点
轴上的椭圆,所以③错误;对于④,设动点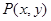 ,则由
,则由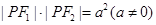 可得
可得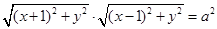 ,将
,将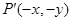 代入等式左边可得
代入等式左边可得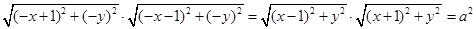 ,所以动点
,所以动点 的轨迹关于原点对称,即④正确;综上可知,真命题的序号是②④.
的轨迹关于原点对称,即④正确;综上可知,真命题的序号是②④.
考点:1.双曲线的定义;2.动点的轨迹问题;3.双曲线的离心率.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,则实数m的值为 .
,则实数m的值为 .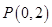 ,抛物线
,抛物线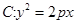
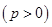 的焦点
的焦点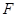 ,线段
,线段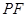 与抛物线
与抛物线 的交点为
的交点为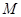 ,过
,过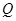 ,若
,若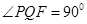 ,则
,则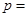 _______.
_______.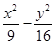 =1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,则实数m的取值范围是________.
=1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,则实数m的取值范围是________. 上的点.若F1、F2是椭圆的两个焦点,则|PF1|+|PF2|=________.
上的点.若F1、F2是椭圆的两个焦点,则|PF1|+|PF2|=________. =1(a>b>0)的左、右焦点,A、B分别是此椭圆的右顶点和上顶点,P是椭圆上一点,O是坐标原点,OP∥AB,PF1⊥x轴,F1A=
=1(a>b>0)的左、右焦点,A、B分别是此椭圆的右顶点和上顶点,P是椭圆上一点,O是坐标原点,OP∥AB,PF1⊥x轴,F1A=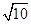 +
+ ,则此椭圆的方程是________________.
,则此椭圆的方程是________________. +
+ =1(a>b>0)的两个焦点,P为椭圆C上一点,且
=1(a>b>0)的两个焦点,P为椭圆C上一点,且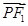 ⊥
⊥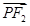 ,若△PF1F2的面积为9,则b= .
,若△PF1F2的面积为9,则b= .