Question

已知F₁、F₂是椭圆的两个焦点，满足

MF1

•

MF2

=0的点M总在椭圆内部，则椭圆离心率的取值范围是

 

．

Answer 1

分析：设椭圆的方程为

x2

a2

+

y2

b2

=1，根据题意可得点M在以为F₁F₂直径的圆上运动且这个圆上的点都在椭圆内部．由此建立a、b、c的不等式，解出a＞

2

c．再利用离心率的公式加以计算，可得此椭圆离心率的取值范围．

解答：解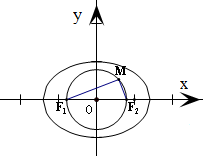：设椭圆的方程为

x2

a2

+

y2

b2

=1（a＞b＞0），焦点为F₁（-c，0）、F₂（c，0），如图所示．
若点M满足

MF1

•

MF2

=0，则

MF1

⊥

MF2

，
可得点M在以为F₁F₂直径的圆上运动，
∵满足

MF1

•

MF2

=0的点M总在椭圆内部，
∴以为F₁F₂直径的圆是椭圆内部的一个圆，即椭圆短轴的端点在椭圆内．
由此可得b＞c，即

a2-c2

c，解之得a＞

2

c．
因此椭圆的离心率e=

c

a

＜

2

2

，椭圆离心率的取值范围是（0，

2

2

）．
故答案为：（0，

2

2

）

点评：本题给出椭圆满足的条件，求椭圆的离心率的范围．着重考查了向量数量积的运算性质、椭圆的标准方程与简单性质等知识，属于中档题．