题目内容
已知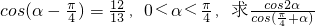 .
.
解:由cos( )=
)= (cosα+sinα)=
(cosα+sinα)= ,
,
得到cosα+sinα= ,
,
两边平方得:(cosα+sinα)2=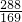 ,
,
∴1+2cosαsinα=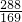 ,即2cosαsinα=
,即2cosαsinα=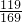 ,
,
∴(cosα-sinα)2=1-2cosαsinα=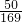 ,
,
又0<α< ,∴cosα-sinα>0,
,∴cosα-sinα>0,
∴cosα-sinα= ,
,
∴cos2α=cos2α-sin2α=(cosα+sinα)(cosα-sinα)= ,
,
cos( )=
)= (cosα-sinα)=
(cosα-sinα)= ,
,
则 =
= ×
×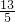 =
= .
.
分析:利用两角和与差的余弦函数公式及特殊角的三角函数值化简已知的等式,得到cosα+sinα的值,然后把得到关系式两边平方,利用完全平方公式及同角三角函数间的基本关系变形,可得出(cosα-sinα)2的值,由α的范围,得到cosα-sinα大于0,开方可得cosα-sinα的值,然后把所求的式子分子利用二倍角的余弦函数公式及平方差化简,将cosα+sinα及cosα-sinα的值代入求出分子的值,分母利用两角和与差的余弦函数公式及特殊角的三角函数值化简,将cosα-sinα的值代入求出分母的值,进而求出所求式子的值.
点评:此题考查了两角和与差的余弦函数公式,同角三角函数间的基本关系,以及二倍角的余弦函数公式,熟练掌握公式及基本关系是解本题的关键,同时注意角度的范围.
 )=
)= (cosα+sinα)=
(cosα+sinα)= ,
,得到cosα+sinα=
 ,
,两边平方得:(cosα+sinα)2=
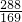 ,
,∴1+2cosαsinα=
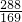 ,即2cosαsinα=
,即2cosαsinα=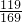 ,
,∴(cosα-sinα)2=1-2cosαsinα=
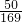 ,
,又0<α<
 ,∴cosα-sinα>0,
,∴cosα-sinα>0,∴cosα-sinα=
 ,
,∴cos2α=cos2α-sin2α=(cosα+sinα)(cosα-sinα)=
 ,
,cos(
 )=
)= (cosα-sinα)=
(cosα-sinα)= ,
,则
 =
= ×
×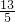 =
= .
.分析:利用两角和与差的余弦函数公式及特殊角的三角函数值化简已知的等式,得到cosα+sinα的值,然后把得到关系式两边平方,利用完全平方公式及同角三角函数间的基本关系变形,可得出(cosα-sinα)2的值,由α的范围,得到cosα-sinα大于0,开方可得cosα-sinα的值,然后把所求的式子分子利用二倍角的余弦函数公式及平方差化简,将cosα+sinα及cosα-sinα的值代入求出分子的值,分母利用两角和与差的余弦函数公式及特殊角的三角函数值化简,将cosα-sinα的值代入求出分母的值,进而求出所求式子的值.
点评:此题考查了两角和与差的余弦函数公式,同角三角函数间的基本关系,以及二倍角的余弦函数公式,熟练掌握公式及基本关系是解本题的关键,同时注意角度的范围.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力.每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.021 | 0.027 | 0.243 | 0.729 |
已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
A、(-∞,-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、(-
|
已知函数f(x)=
若f(2-a2)>f(a),则实数a的取值范围是( )
|
| A、(-∞,-1)∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-∞,-2)∪(1,+∞) |