Question

18.

    在△ABC中，已知，求△ABC的面积.

Answer 1

18.本小题主要考查正弦定理、余弦定理和三角形面积公式等基础知识，同时考查利用三角公式进行恒等变形的技能和运算能力.

解法1：设AB、BC、CA的长分别为c、a、b，

.

 

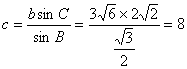故所求面积

解法2：同解法1可得c=8.

又由余弦定理可得，a²=b²+c²-2bccosA.

而cosA=-cos(B+C)=-cosBcosC+sinBsinC

=-

∴a²=(3)²+8²-2×3×8×（）=22+8。

∵a>0，∴a==4+.

故所求面积S_△ABC=acsinB=6+8.

解法3：同解法1可得c=8.

又由余弦定理可得

∵

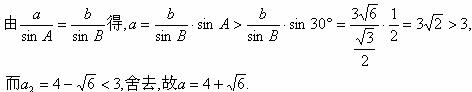
故所求面积