题目内容
在等比数列 中,
中, 则
则
A. | B. | C. | D. |
A
解析试题分析:因为根据题意可知等比数列 中,结合其通项公式可知,
中,结合其通项公式可知, ,而对于
,而对于 ,故选A
,故选A
考点:本题主要考查等比数列的通项公式的求解和运用。
点评:解决该试题的关键是根据已知中两项之间的关系式可知其公比的立方,然后结合通项公式的性质 来得到结论。
来得到结论。

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
数列 为等比数列,
为等比数列, 为其前
为其前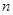 项和,已知
项和,已知 ,则公比
,则公比
A. | B. | C. 或 或 | D. 或 或 |
设等比数列 中,前n项和为
中,前n项和为 ,已知
,已知 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知等比数列 中,各项都是正数,而且
中,各项都是正数,而且 成等差数列,则
成等差数列,则 ( )
( )
A. | B. | C. | D. |
记等比数列 的前
的前 项和为
项和为 ,若
,若 则
则 ( )
( )
| A. 9 | B.27 | C. 8 8 | D.8 |
若等比数列 的前
的前 项和
项和 ,则
,则 = ( )
= ( )
| A.0 | B.-1 | C.1 | D.3 |
 满足
满足 且A、B、C三点共线,则S2006=
且A、B、C三点共线,则S2006=  的左右焦点分别为
的左右焦点分别为 ,P是椭圆上的一点,且
,P是椭圆上的一点,且 成等比数列,则椭圆的离心率的取值范围为( )
成等比数列,则椭圆的离心率的取值范围为( )



 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )


