题目内容
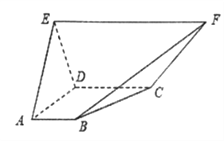
【题目】在如图所示的五面体中,面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
, ![]() ,△ADE是边长为2的正三角形.
,△ADE是边长为2的正三角形.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求点B到平面ACF的距离.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)做辅助线,构造线面垂直,取![]() 的中点
的中点![]() ,连接
,连接![]() ,先证
,先证 ![]() 平面
平面![]() 得到
得到![]() ,再通过相似证得
,再通过相似证得![]() ,故得到线面垂直,再推线线垂直。(2)承接第一问的结论,因为
,故得到线面垂直,再推线线垂直。(2)承接第一问的结论,因为![]() 平面
平面![]() ,故直接由B点做AF的垂线即可,垂线就是BE,再根据梯形的边长求出即可。
,故直接由B点做AF的垂线即可,垂线就是BE,再根据梯形的边长求出即可。
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,依题意易知
,依题意易知![]() ,
,
平面![]() 平面
平面![]() 平面
平面![]()
![]() .
.
又![]()
![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .
.
在![]() 和
和![]() 中,
中, ![]()
![]() .
.
因为![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由第一问知道![]() 平面
平面![]() ,故点B到平面ACF的距离,直接连BE交AF于点M,则BM就是要求的距离,在梯形ABFE中,求得BE=
,故点B到平面ACF的距离,直接连BE交AF于点M,则BM就是要求的距离,在梯形ABFE中,求得BE=![]() 。
。

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目