题目内容
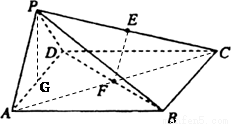
如图所示,在四棱锥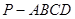 中,底面ABCD是边长为a的正方形,侧面
中,底面ABCD是边长为a的正方形,侧面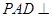 底面ABCD,且
底面ABCD,且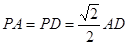 ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.
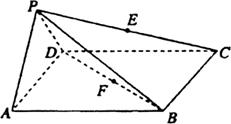
(1)求证: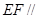 平面PAD;
平面PAD;
(2)求证:平面PDC 平面PAD;
平面PAD;
(3)求四棱锥 的体积.
的体积.
(1)先证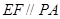 ,再根据线面平行的判定定理即可证明;
,再根据线面平行的判定定理即可证明;
(2)先证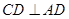 ,进而证明
,进而证明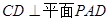 ,再根据面面垂直的判定定理即可证明;
,再根据面面垂直的判定定理即可证明;
(3)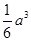
【解析】
试题分析:(1)连接EF,AC
∵四棱锥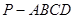 中,底面ABCD是边长为a的正方形且点F为对角线BD的中点,
中,底面ABCD是边长为a的正方形且点F为对角线BD的中点,
∴对角线AC经过F点, ……1分
又在 中,点E为PC的中点,
中,点E为PC的中点,
∴EF为 的中位线,
的中位线,
∴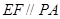 , ……2分
, ……2分
又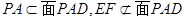 , ……3分
, ……3分
∴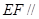 平面PAD. ……4分
平面PAD. ……4分
(2)∵底面ABCD是边长为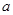 的正方形
的正方形
∴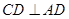 , ……5分
, ……5分
又侧面 底面ABCD,
底面ABCD, ,侧面
,侧面 底面ABCD=AD,
底面ABCD=AD,
∴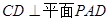 . ……7分
. ……7分
又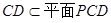
∴平面PDC 平面PAD
. ……8分
平面PAD
. ……8分
(3)过点P作AD的垂线PG,垂足为点G,
∵侧面 底面ABCD,
底面ABCD,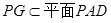 ,侧面
,侧面 底面ABCD=AD,
底面ABCD=AD,
∴ ,即PG为四棱锥
,即PG为四棱锥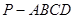 的高, ……9分
的高, ……9分
又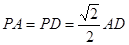 且AD=a,
且AD=a,
∴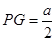 , ……10分
, ……10分
∴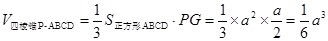 。 ……12分
。 ……12分
考点:本小题主要考查线面平行、面面垂直的证明和体积的计算.
点评:证明线面平行、面面垂直时要紧扣相应的判定定理和性质定理,定理中的条件要一一列出来,缺一不可,如证明线面平行时,要强调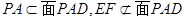 .
.

 阅读快车系列答案
阅读快车系列答案 中,底面四边形
中,底面四边形 是菱形,
是菱形, ,
, 是边长为2的等边三角形,
是边长为2的等边三角形,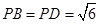 ,
,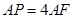 .
.
 底面
底面 与平面
与平面 所成角的大小;
所成角的大小;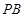 上是否存在一点
上是否存在一点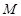 ,使得
,使得 ∥平面
∥平面 ?如果存在,求
?如果存在,求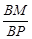 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由. 中,
中, 平面
平面 ,
, ,
, ,
, ,
, 是
是 的中点.
的中点. 平面
平面 ;
;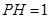 ,
, ,
, ,求二面角
,求二面角 的正切值.
的正切值.
 中,底面ABCD是矩形,
中,底面ABCD是矩形,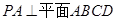 ,
, 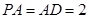 ,
,
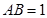 ,
, 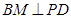 , 垂足为
, 垂足为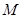 ,
,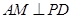 ;
;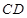 与平面
与平面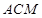 所成角的余弦值。
所成角的余弦值。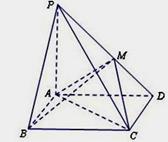
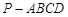 中,
中,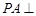 平面
平面 ,底面
,底面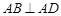 ,
,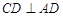 。
。 平面
平面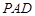 ;
;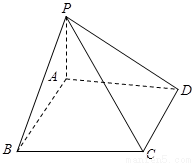
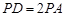 ,求二面角
,求二面角 的大小。
的大小。