题目内容
10.已知f(x)=2x+m,g(x)=x2+mx+m(m,n∈R,m2≠n2),如果对任意的实数x,恒有f(x)≤g(x),那么当不等式k(n+m)≥$\frac{g(n)-g(m)}{n-m}$恒成立时,实数k的最小值为1.分析 利用对任意的实数x,恒有f(x)≤g(x),求出m的值,不等式k(n+m)≥$\frac{g(n)-g(m)}{n-m}$恒成立,即不等式k≥$\frac{n+4}{n+2}$=1+$\frac{2}{n+2}$(n+2>0)恒成立,求出右边1+$\frac{2}{n+2}$>1,即可求出实数k的最小值.
解答 解:∵对任意的实数x,恒有f(x)≤g(x),
∴x2+(m-2)x≥0,
∴m=2,
不等式k(n+m)≥$\frac{g(n)-g(m)}{n-m}$恒成立,即不等式k≥$\frac{n+4}{n+2}$=1+$\frac{2}{n+2}$(n+2>0)恒成立
∴k≥1.
∴实数k的最小值为1.
故答案为:1.
点评 本题考查恒成立问题,考查分离参数法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
5.若函数f(x)=x3-x-a恰好有三个不同的零点,则这三个零点的和为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 与a有关 |
20.已知直线a⊥直线b,b⊥直线c,c⊥a,直线l与a,b所成的角分别为45°,60°,则l与c所成的角为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
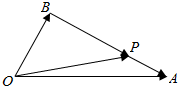 如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.
如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.