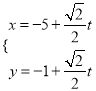题目内容
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .直线
.直线![]() 过点
过点![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
【答案】(1)2;(2)16.
【解析】试题分析:(1)将直线l和椭圆C的转化为普通方程,左焦点F在直线l上,求解出直线1方程与椭圆C联立方程组,求解A,B坐标,利用两点之间的距离公式求解|FA||FB|的值.
(2)设椭圆在第一象限上一点P(acosθ,bsinθ),内接矩形周长为: ![]() ,即得答案.
,即得答案.
试题解析:
(1)已知曲线![]() 的标准方程为
的标准方程为 ![]() ,则其左焦点为
,则其左焦点为![]() ,则
,则![]() ,将直线
,将直线![]() 的参数方程
的参数方程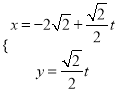 与曲线
与曲线![]() 的方程
的方程 ![]() 联立,得
联立,得![]() ,则
,则![]() .
.
(2)由曲线![]() 的方程为
的方程为 ![]() ,可设曲线
,可设曲线![]() 上的动点
上的动点![]() ,则以
,则以![]() 为顶点的内接矩形周长为
为顶点的内接矩形周长为![]() ,因此该内接矩形周长的最大值为
,因此该内接矩形周长的最大值为![]() .
.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度/ | -5 | 0 | 4 | 7 | 12 | 15 | 19 | 23 | 27 | 31 | 36 |
热饮杯数 | 156 | 150 | 132 | 128 | 130 | 116 | 104 | 89 | 93 | 76 | 54 |
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;
(3)求回归方程;
(4)如果某天的气温是![]() ,预测这天卖出的热饮杯数.
,预测这天卖出的热饮杯数.