题目内容
在△ABC中，已知角B=45°，D是BC边上一点，AD=5，AC=7，DC=3，求AB?
解：如题图，在△ACD中，由余弦定理可得cos∠ADC=
=
．
∵0°＜∠ADC＜180°，∴∠ADC=120°，∴∠ADB=60°．
在△ABD中，由正弦定理可得
，解得AB=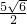
．
∴AB=．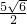
分析：在△ACD中，由余弦定理可得cos∠ADC，得出∠ADC，从而得出∠ADB，在△ABD中，由正弦定理即可得出AB．
点评：熟练掌握余弦定理和正弦定理是解题的关键．
=．∵0°＜∠ADC＜180°，∴∠ADC=120°，∴∠ADB=60°．
在△ABD中，由正弦定理可得
，解得AB=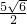．∴AB=
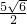．分析：在△ACD中，由余弦定理可得cos∠ADC，得出∠ADC，从而得出∠ADB，在△ABD中，由正弦定理即可得出AB．
点评：熟练掌握余弦定理和正弦定理是解题的关键．
练习册系列答案
黎明文化寒假作业系列答案
相关题目