题目内容
【题目】如图,圆锥PO中,AB是圆O的直径,且AB=4,C是底面圆O上一点,且AC=2![]() ,点D为半径OB的中点,连接PD.
,点D为半径OB的中点,连接PD.
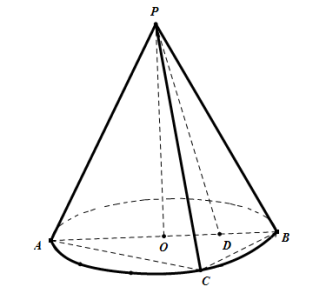
(1)求证:PC在平面APB内的射影是PD;
(2)若PA=4,求底面圆心O到平面PBC的距离.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由题意推导出△BOC是正三角形,CD⊥OB,OP⊥CD,从而CD⊥平面PAB,即可得证;
(2)设点O到平面PBC的距离为d,由题意可得![]() ,
,![]() ,由
,由![]() ,即可得解.
,即可得解.
(1)证明:连接CD、OC,如图:

∵AB=4,![]() ,AC⊥BC,∴
,AC⊥BC,∴![]() ,
,
∵OB=OC,∴△BOC是正三角形,
又D点是OB的中点,∴CD⊥OB,
又PO⊥平面ABC,∴OP⊥CD,
∵OP∩OB=O,∴CD⊥平面PAB,
∴PC在平面APB内的射影是PD;
(2)由PA=4,可知![]() ,PB=PC=4,
,PB=PC=4,
∴![]() ,
,![]() ,
,
∴![]() ,
,
设点O到平面PBC的距离为d,
则![]() ,解得
,解得![]() ,
,
∴底面圆心O到平面PBC的距离为![]() .
.

练习册系列答案
相关题目