题目内容
过点Q(-2, ) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
(1)求γ的值;
(2)设P是圆C上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y 轴于点B,设 =
= +
+ ,求|
,求| |的最小值(O为坐标原点).
|的最小值(O为坐标原点).
解:(1)圆C:x2+y2=r2(r>0)的圆心为O(0,0),则
∵过点Q(-2, ) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4
) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4
∴r=OD=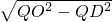 =
=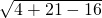 =3;
=3;
(2)设直线l的方程为 (a>0,b>0),即bx+ay-ab=0,则A(a,0),B(0,b),
(a>0,b>0),即bx+ay-ab=0,则A(a,0),B(0,b),
∵ =
= +
+ ,∴
,∴ =(a,b),∴
=(a,b),∴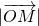 =
=
∵直线l与圆C相切,∴
∴3 =ab≤
=ab≤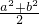
∴a2+b2≥36
∴
当且仅当 时,
时,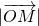 的最小值为6.
的最小值为6.
分析:(1)利用圆的切线的性质,结合勾股定理,可求r的值;
(2)设出直线方程,利用 =
= +
+ ,表示出
,表示出 ,求出模长,利用基本不等式即可求得结论.
,求出模长,利用基本不等式即可求得结论.
点评:本题考查圆的切线的性质,考查向量知识的运用,考查基本不等式,属于中档题.
∵过点Q(-2,
 ) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4
) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4∴r=OD=
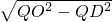 =
=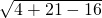 =3;
=3;(2)设直线l的方程为
 (a>0,b>0),即bx+ay-ab=0,则A(a,0),B(0,b),
(a>0,b>0),即bx+ay-ab=0,则A(a,0),B(0,b),∵
 =
= +
+ ,∴
,∴ =(a,b),∴
=(a,b),∴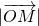 =
=
∵直线l与圆C相切,∴

∴3
 =ab≤
=ab≤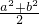
∴a2+b2≥36
∴

当且仅当
 时,
时,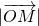 的最小值为6.
的最小值为6.分析:(1)利用圆的切线的性质,结合勾股定理,可求r的值;
(2)设出直线方程,利用
 =
= +
+ ,表示出
,表示出 ,求出模长,利用基本不等式即可求得结论.
,求出模长,利用基本不等式即可求得结论.点评:本题考查圆的切线的性质,考查向量知识的运用,考查基本不等式,属于中档题.

练习册系列答案
相关题目
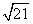 )作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4,
)作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4,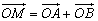 ,求
,求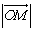 的最小值(O为坐标原点)。
的最小值(O为坐标原点)。 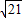 ) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4.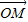 =
=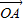 +
+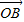 ,求|
,求| |的最小值(O为坐标原点).
|的最小值(O为坐标原点).