题目内容
在直角坐标坐标系中,已知一个圆心在坐标原点,半径为2的圆,从这个圆上任意一点P向y轴作垂线段![]() 为垂足.
为垂足.
(1)求线段![]() 中点M的轨迹C的方程;
中点M的轨迹C的方程;
(2)过点Q(一2,0)作直线l与曲线C交于A、B两点,设N是过点(![]() ,0),且以言
,0),且以言![]() 为方向向量的直线上一动点,满足
为方向向量的直线上一动点,满足![]() (O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线Z的方程;若不存在,说明理由.
(O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线Z的方程;若不存在,说明理由.
解:(1)设M(x,y)是所求曲线上的任意一点,P(![]() )是方程
)是方程![]() 的圆上的任意一点,则
的圆上的任意一点,则![]() .
.
则有: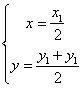 ,即
,即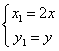 ,代入
,代入![]() 得,
得,
轨迹C 的方程为![]() .
.
(2)当直线l的斜率不存在时,与椭圆无交点.
所以设直线l的方程为y=k(x+2),与椭圆交于![]() 两点,N点所在直线方程为
两点,N点所在直线方程为![]() .
.
由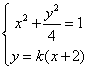 得(4+
得(4+![]() )
)![]() .
.
由![]() ∴
∴![]() .
.
即![]()
![]()
![]() ,即
,即![]() ,∴四边形OANB为平行四边形
,∴四边形OANB为平行四边形
假设存在矩形OANB,则![]() ,即
,即![]() ,
,
即![]() ,
,
于是有![]() 得
得![]() .
.
设N(![]() ),由
),由![]() 得
得![]() ,
,
即点N在直线x=-![]() 上. ∴存在直线l使四边形OANB为矩形,
上. ∴存在直线l使四边形OANB为矩形,
直线l的方程为![]() .
.

练习册系列答案
相关题目
 ,0),且以
,0),且以 为方向向量的直线上一动点,满足
为方向向量的直线上一动点,满足 (O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由。
(O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由。 ,0),且以言
,0),且以言 为方向向量的直线上一动点,满足
为方向向量的直线上一动点,满足 (O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线Z的方程;若不存在,说明理由.
(O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线Z的方程;若不存在,说明理由. ,0),且以言
,0),且以言 为方向向量的直线上一动点,满足
为方向向量的直线上一动点,满足 (O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线Z的方程;若不存在,说明理由.
(O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线Z的方程;若不存在,说明理由.