题目内容
已知集合 ,
, ,设
,设 是等差数列
是等差数列 的前
的前 项和,若
项和,若 的任一项
的任一项 ,首项
,首项 是
是 中的最大数, 且
中的最大数, 且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,令
,令
 ,试比较
,试比较 与
与 的大小.
的大小.
解: (Ⅰ)根据题设可得: 集合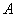 中所有的元素可以组成以
中所有的元素可以组成以 为首项,
为首项, 为公差的递减等差数列;集合
为公差的递减等差数列;集合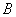 中所有的元素可以组成以
中所有的元素可以组成以 为首项,
为首项, 为公差的递减等差数列.
为公差的递减等差数列.
由此可得,对任意的 ,有
,有
 中的最大数为
中的最大数为 ,即
,即
设等差数列 的公差为
的公差为 ,则
,则 ,
,
因为 ,
, 
 ,即
,即
由于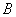 中所有的元素可以组成以
中所有的元素可以组成以 为首项,
为首项, 为公差的递减等差数列
为公差的递减等差数列
所以 ,由
,由
 ,所以
,所以
所以数列 的通项公式为
的通项公式为 (
( )
)
(Ⅱ)
 于是确定
于是确定 与
与 的大小关系等价于比较
的大小关系等价于比较 与
与 的大小
的大小
由 ,
, ,
, ,
, ,
,
可猜想当 时,
时,
证明如下:
证法1:(1)当 时,由上验算可知成立.
时,由上验算可知成立.
(2)假设 时,
时, ,
,
则
所以当 时猜想也成立
时猜想也成立
根据(1)(2)可知 ,对一切 的正整数,都有
的正整数,都有
 当
当 时,
时, ,当
,当 时
时
证法2:当 时
时

 当
当 时,
时, ,当
,当 时
时

练习册系列答案
相关题目
 的焦点
的焦点 、
、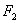 ,点
,点 为其上的动点,当∠
为其上的动点,当∠ ,且
,且 成等比数列,则
成等比数列,则 有
有 B、最小值
B、最小值 C、最大值
C、最大值  的各项都为正数,且当
的各项都为正数,且当 时,
时, ,则数列
,则数列 ,
, ,
, ,
, ,…,
,…, ,…的前
,…的前 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 对任意
对任意 时都有意义,则实数a的范围是( )
时都有意义,则实数a的范围是( ) B.
B. 
 D.
D. 

 的圆柱的侧面积为
的圆柱的侧面积为 B.
B. C.
C. D.
D.