题目内容
若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为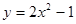 ,值域为
,值域为 的“孪生函数”共有( )
的“孪生函数”共有( )
| A.10个 | B.9个 | C.8个 | D.4个 |
B
解析试题分析:由已知“孪生函数”的定义:一系列函数的解析式相同,值域相同,但定义域不同。当函数解析式为y=2x2-1,值域为{1,7}时,函数的定义域可能为:{-3,-1},{-3,1},{3,-1},{3,1},{-3,-1,1},{-3,-1,3},{-1,1,3},{-3,1,3},{-3,-1,1,3},共9个故选B
考点:函数的三要素。
点评:本题是新定义题型,做此题的关键是迅速理解所给的新定义。此题在列举函数的定义域时,要注意一定的规则,以免重复和遗漏.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 对任意x都有
对任意x都有  ,则
,则 ( )。
( )。
A. | B. 0 | C. 3 | D. |
函数 的图象如右图所示,下列说法正确的是( )
的图象如右图所示,下列说法正确的是( )
①函数 满足
满足
②函数 满足
满足
③函数 满足
满足
④函数 满足
满足
| A.①② | B.②④ | C.①③ | D.③④ |
定义域为R的函数 满足条件:
满足条件:
① ;
;
②
 ; ③
; ③ .
.
则不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |
函数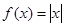 和
和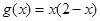 的递增区间依次是( )
的递增区间依次是( )
A.(-∞,0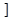 ,(-∞,1 ,(-∞,1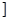 | B.(-∞,0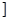 ,[1,+∞ ,[1,+∞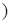 |
C.[0,+∞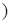 ,(-∞,1 ,(-∞,1 | D.[0,+∞),[1,+∞) |
已知函数 的图象是连续不断的,有如下的
的图象是连续不断的,有如下的 对应值表:
对应值表:
 | 1 | 2 | 3 | 4 | 5 | 6 |
 | 123.56 | 21.45 | -7.82 | 11.57 | -53.76 | -126.49 |
 在区间[1,6]上的零点至少有( )
在区间[1,6]上的零点至少有( )A. 3个 B. 2个 C. 4个 D.5个
下列函数既是奇函数,又是增函数的是( )
A. | B. |
C. | D. |
若f (lnx)=3x+4,则f (x)的表达式为
| A.3lnx | B.3lnx+4 |
| C.3ex | D.3ex+4 |
 的图像大致是 ( )
的图像大致是 ( )