题目内容
若A,B为锐角三角形ABC的两个内角,则点P(sinA-cosB,cosA-sinB)位于( )
分析:由A,B为锐角三角形的两个内角,知A+B>
,所以sinA-cosB>0,同理可得cosA-sinB<0,由此能求出点P所在的象限.
| π |
| 2 |
解答:解:∵A,B为锐角三角形的两个内角,
∴A+B>
,
∴
>A>
-B>0,
∴sinA>sin(
-B)=cosB,
∴sinA-cosB>0,
同理可得cosA-sinB<0,
故选D.
∴A+B>
| π |
| 2 |
∴
| π |
| 2 |
| π |
| 2 |
∴sinA>sin(
| π |
| 2 |
∴sinA-cosB>0,
同理可得cosA-sinB<0,
故选D.
点评:本题考查三角函数值的符号,解题时要认真审题,仔细解答.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
若A,B为锐角三角形的两个锐角,则tanAtanB的值( )
| A、不大于1 | B、小于1 | C、等于1 | D、大于1 |
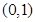 的函数
的函数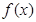 ,对于任意
,对于任意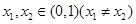 ,恒有
,恒有 . 若A、B为锐角三角形ABC的两内角,则有( )
. 若A、B为锐角三角形ABC的两内角,则有( ) B、
B、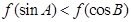
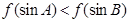 D、
D、