题目内容
a、b、c∈R，且b＞0．已知函数f（x）=a+bsinx+ccosx的图象经过点A（0，1），
；又函数f（x）的最大值为
，求f（x）的解析式．
解：f（x）=a+bsinx+ccosx的图象经过点A（0，1）、B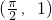
∴
，b=c（2分）
∵且b＞0
∴f（x）的最大值为
可得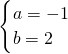
∴f（x）=-1+2（sinx+cosx）（8分）
分析：将点A（0，1），代入函数解析式，得出b=c，继续将f（x）化为
利用三角函数的性质求最值，求出a，b，c即可．
点评：本题考查特殊角的三角函数值，三角函数公式的应用、三角函数的性质，将f（x）化为一角一函数是关键．
∴
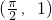
，b=c（2分）∵且b＞0
∴f（x）的最大值为
可得
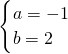
∴f（x）=-1+2（sinx+cosx）（8分）
分析：将点A（0，1），
代入函数解析式，得出b=c，继续将f（x）化为利用三角函数的性质求最值，求出a，b，c即可．
点评：本题考查特殊角的三角函数值，三角函数公式的应用、三角函数的性质，将f（x）化为一角一函数是关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目