题目内容
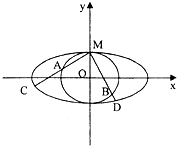 (2013•东莞二模)如图,圆O与离心率为
(2013•东莞二模)如图,圆O与离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆T与圆O的方程;
(2)过点M引两条互相垂直的两直线l1、l2与两曲线分别交于点A、C与点B、D(均不重合).
①若P为椭圆上任一点,记点P到两直线的距离分别为d1、d2,求
| d | 2 1 |
| d | 2 2 |
②若3
| MA |
| MC |
| MB |
| MD |
分析:(1)由题意可知圆的半径等于1,椭圆的短半轴等于1,根据e=
=
,结合a2=b2+c2求出椭圆的长半轴,则椭圆方程和圆的方程可求;
(2)①因为两直线l1、l2相互垂直,所以点P到两直线的距离d1、d2的平方和可转化为P点到M点距离的平方,利用点P在椭圆上把要求的式子化为含P点纵坐标的函数,利用二次函数可求最大值;
②设出直线l1的方程,分别和圆的方程及椭圆方程联立A,C点的坐标,利用置换k的方法求出B,D点的坐标,分别写出向量
,
,
,
的坐标,代入若3
•
=4
•
中求出k的值,则l1与l2的方程的方程可求.
| c |
| a |
| ||
| 2 |
(2)①因为两直线l1、l2相互垂直,所以点P到两直线的距离d1、d2的平方和可转化为P点到M点距离的平方,利用点P在椭圆上把要求的式子化为含P点纵坐标的函数,利用二次函数可求最大值;
②设出直线l1的方程,分别和圆的方程及椭圆方程联立A,C点的坐标,利用置换k的方法求出B,D点的坐标,分别写出向量
| MA |
| MC |
| MB |
| MD |
| MA |
| MC |
| MB |
| MD |
解答:解:(1)由题意知:
=
,b=1.
又a2=b2+c2,所以a2=c2+1,
联立
,解得a=2,c=
所以椭圆C的方程为
+y2=1.圆O的方程x2+y2=1;
(2)①设P(x0,y0)因为l1⊥l2,则d12+d22=PM2=x02+(y0-1)2,
因为
+
=1,所以d12+d22=4-4y02+(y0-1)2=-3(y0+
)2+
,
因为-1≤y0≤1,所以当y0=
时,
+
取得最大值为
,此时点P(±
,
).
②设l1的方程为y=kx+1,
由
,得:(k2+1)x2+2kx=0,由xA≠0,所以xA=-
,
代入y=kx+1得:yA=
.
所以A(-
,
).
由
,得(4k2+1)x2+8kx=0,由xC≠0,所以xC=-
,
代入y=kx+1得:yC=
.
所以C(-
,
).
把A,C中的k置换成-
可得B(
,
),D(
,
)
所以
=(-
,
),
=(
,
)
=(
,
),
=(
,
)
由3
=4
•
,
得3[(-
)(-
)+(-
)(-
)]
=4[
•
+(-
)(-
)],
整理得:
=
,即3k4-4k2-4=0,解得k=±
.
所以l1的方程为y=
x+1,l2的方程为y=-
x+1
或l1的方程为y=-
x+1,l2的方程为y=
x+1.
| c |
| a |
| ||
| 2 |
又a2=b2+c2,所以a2=c2+1,
联立
|
| 3 |
所以椭圆C的方程为
| x2 |
| 4 |
(2)①设P(x0,y0)因为l1⊥l2,则d12+d22=PM2=x02+(y0-1)2,
因为
| ||
| 4 |
| y | 2 0 |
| 1 |
| 3 |
| 16 |
| 3 |
因为-1≤y0≤1,所以当y0=
| 1 |
| 3 |
| d | 2 1 |
| d | 2 2 |
| 16 |
| 3 |
4
| ||
| 3 |
| 1 |
| 3 |
②设l1的方程为y=kx+1,
由
|
| 2k |
| k2+1 |
代入y=kx+1得:yA=
| 1-k2 |
| 1+k2 |
所以A(-
| 2k |
| k2+1 |
| 1-k2 |
| 1+k2 |
由
|
| 8k |
| 4k2+1 |
代入y=kx+1得:yC=
| 1-4k2 |
| 1+4k2 |
所以C(-
| 8k |
| 4k2+1 |
| 1-4k2 |
| 1+4k2 |
把A,C中的k置换成-
| 1 |
| k |
| 2k |
| k2+1 |
| k2-1 |
| k2+1 |
| 8k |
| k2+4 |
| k2-4 |
| k2+4 |
所以
| MA |
| 2k |
| k2+1 |
| -2k2 |
| 1+k2 |
| MC |
| -8k |
| 4k2+1 |
| -8k2 |
| 4k2+1 |
| MB |
| 2k |
| k2+1 |
| -2 |
| k2+1 |
| MD |
| 8k |
| k2+4 |
| -8 |
| k2+4 |
由3
| MA• |
| MC |
| MB |
| MD |
得3[(-
| 2k |
| k2+1 |
| 8k |
| 4k2+1 |
| 2k2 |
| 1+k2 |
| 8k2 |
| 1+4k2 |
=4[
| 2k |
| k2+1 |
| 8k |
| k2+4 |
| 2 |
| k2+1 |
| 8 |
| k2+4 |
整理得:
| 3k2 |
| 1+4k2 |
| 4 |
| k2+4 |
| 2 |
所以l1的方程为y=
| 2 |
| ||
| 2 |
或l1的方程为y=-
| 2 |
| ||
| 2 |
点评:本题考查了圆的标准方程,椭圆的标准方程,直线和圆锥曲线的位置关系,考查了数学转化思想和方程思想方法,训练了学生的计算能力,属难题.

练习册系列答案
相关题目
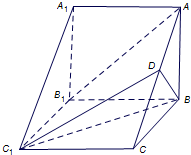 (2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.