题目内容
 (本题满分12分)如图,四棱锥P—ABCD中,PA⊥ABCD,四边形ABCD 是矩形. E、F分别是AB、PD的中点.若PA=AD=3,CD=
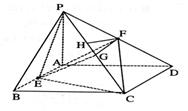
(本题满分12分)如图,四棱锥P—ABCD中,PA⊥ABCD,四边形ABCD 是矩形. E、F分别是AB、PD的中点.若PA=AD=3,CD=![]() . (1)求证:AF//平面PCE;
. (1)求证:AF//平面PCE;
(2)求点A到平面PCE的距离;(3)求直线FC与平面PCE所成角的大小。
(2)![]() (3)
(3)![]()
解析:
:解法一:(1)取PC的中点G,连结EG,FG,又由F为PD中点,则FG//![]()
| |
|
|
(2)由(1)知点A到平面PCE的距离等于点F到
平面PCE的距离,所以只要求出点F到平面PCE的距离即可。
![]()
![]()
![]()
![]()
![]()
![]()
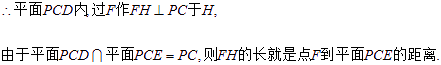
又已知得:![]() .
.
![]() .
. ![]() .
. ![]() .
.
![]() 8分
8分
(3)由(2)知![]()
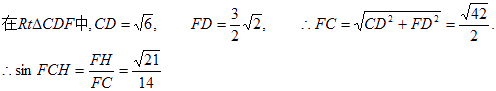
![]() 12分
12分
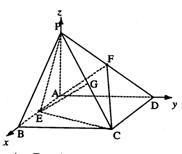
解法二:如图建立空间直角坐标系![]() ,A(0,0,0),P(0,0,3),D(0,3,0),E(
,A(0,0,0),P(0,0,3),D(0,3,0),E(![]() ,0,0),F(0,
,0,0),F(0,![]() ,
,![]() ),C(
),C(![]() ,3,0) 2分
,3,0) 2分
|
![]() ,
,![]()
即![]() ,又
,又![]()
![]() 4分
4分
(2)设平面![]() 的法向量
的法向量![]() .
.
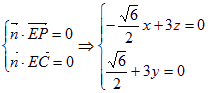 ,取
,取![]()
又![]() ,故
,故![]() 到平面
到平面![]() 的距离为
的距离为![]() 8分
8分
(3)![]()
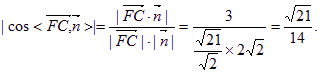
![]() 直线FC与平面PCE所成角的大小为
直线FC与平面PCE所成角的大小为![]() . 12分
. 12分

练习册系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
