题目内容
(本小题满分12分)已知抛物线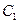 :
: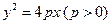 ,焦点为
,焦点为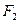 ,其准线与
,其准线与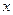 轴交于点
轴交于点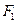 ;椭圆
;椭圆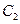 :分别以
:分别以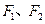 为左、右焦点,其离心率
为左、右焦点,其离心率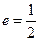 ;且抛物线
;且抛物线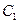 和椭圆
和椭圆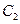 的一个交点记为
的一个交点记为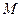 .
.
(1)当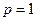 时,求椭圆
时,求椭圆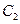 的标准方程;
的标准方程;
(2)在(1)的条件下,若直线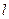 经过椭圆
经过椭圆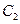 的右焦点
的右焦点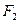 ,且与抛物线
,且与抛物线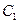 相交于
相交于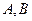 两点,若弦长
两点,若弦长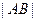 等于
等于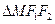 的周长,求直线
的周长,求直线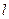 的方程.
的方程.
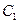 :
: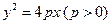 ,焦点为
,焦点为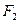 ,其准线与
,其准线与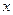 轴交于点
轴交于点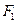 ;椭圆
;椭圆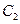 :分别以
:分别以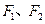 为左、右焦点,其离心率
为左、右焦点,其离心率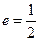 ;且抛物线
;且抛物线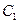 和椭圆
和椭圆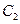 的一个交点记为
的一个交点记为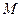 .
.(1)当
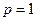 时,求椭圆
时,求椭圆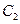 的标准方程;
的标准方程;(2)在(1)的条件下,若直线
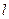 经过椭圆
经过椭圆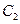 的右焦点
的右焦点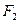 ,且与抛物线
,且与抛物线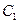 相交于
相交于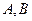 两点,若弦长
两点,若弦长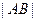 等于
等于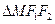 的周长,求直线
的周长,求直线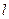 的方程.
的方程. (1)
 =1
=1(2)

(1)当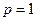 时,F
时,F (1,0),F
(1,0),F (-1,0)
(-1,0)
设椭圆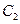 的标准方程为
的标准方程为 (
( >
> >0),∴
>0),∴ =1,
=1, =
=
∵ ,∴
,∴ =2,
=2, =
=
故椭圆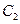 的标准方程为
的标准方程为 ="1. " ……….4分
="1. " ……….4分
(2) (ⅰ)若直线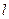 的斜率不存在,则
的斜率不存在,则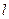 :
: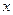 =1,且A(1,2),B(1,-2),∴
=1,且A(1,2),B(1,-2),∴ =4
=4
又∵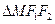 的周长等于
的周长等于 =2
=2 +2
+2 =6
=6

∴直线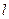 的斜率必存在. ………6分
的斜率必存在. ………6分
(ⅱ)设直线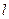 的斜率为
的斜率为 ,则
,则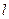 :
:
由 ,得
,得
∵直线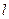 与抛物线
与抛物线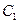 有两个交点A,B
有两个交点A,B
 ∴
∴ ,且
,且
设则可得 ,
,
于是 =
= =
=
=
= =
=
∵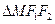 的周长等于
的周长等于 =2
=2 +2
+2 =6
=6
∴由 =6,解得
=6,解得 =
=
故所求直线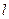 的方程为
的方程为 . …………12分
. …………12分
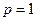 时,F
时,F (1,0),F
(1,0),F (-1,0)
(-1,0) 设椭圆
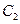 的标准方程为
的标准方程为 (
( >
> >0),∴
>0),∴ =1,
=1, =
=
∵
 ,∴
,∴ =2,
=2, =
=
故椭圆
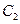 的标准方程为
的标准方程为 ="1. " ……….4分
="1. " ……….4分 (2) (ⅰ)若直线
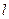 的斜率不存在,则
的斜率不存在,则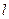 :
: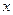 =1,且A(1,2),B(1,-2),∴
=1,且A(1,2),B(1,-2),∴ =4
=4又∵
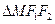 的周长等于
的周长等于 =2
=2 +2
+2 =6
=6

∴直线
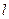 的斜率必存在. ………6分
的斜率必存在. ………6分 (ⅱ)设直线
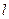 的斜率为
的斜率为 ,则
,则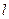 :
:
由
 ,得
,得
∵直线
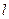 与抛物线
与抛物线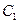 有两个交点A,B
有两个交点A,B ∴
∴ ,且
,且
设则可得
 ,
,
于是
 =
= =
=
=

=
 =
=
∵
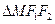 的周长等于
的周长等于 =2
=2 +2
+2 =6
=6∴由
 =6,解得
=6,解得 =
=
故所求直线
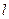 的方程为
的方程为 . …………12分
. …………12分
练习册系列答案
相关题目
 的焦点坐标为( ) .
的焦点坐标为( ) . 



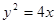 的焦点作直线与抛物线交于
的焦点作直线与抛物线交于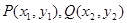 两点,若
两点,若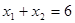 ,则
,则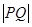 的值为
的值为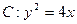 的准线与
的准线与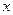 轴交于
轴交于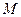 点,
点,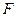 为抛物线
为抛物线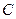 的焦点,过
的焦点,过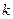 的直线与抛物线
的直线与抛物线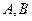 两点。
两点。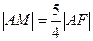 ,求
,求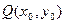 满足
满足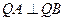 ,若存在,求
,若存在,求
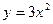 的焦点坐标是_
的焦点坐标是_ ___________________.
___________________.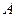 和
和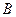 是抛物线
是抛物线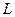 上的两个动点,且在
上的两个动点,且在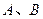 及抛物线
及抛物线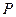 的顶点所成的三角形重心的轨迹也是一抛物线,记为
的顶点所成的三角形重心的轨迹也是一抛物线,记为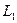 .对
.对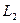 ,余类推.设如此得到抛物线的序列为
,余类推.设如此得到抛物线的序列为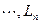 ,若抛物线
,若抛物线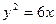 ,经专家计算得,
,经专家计算得,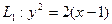 ,
, 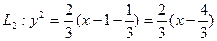 ,
,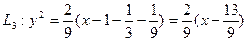 ,
, 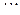 ,
, 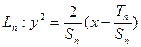 .
.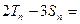 .:Z_x
.:Z_x 的焦点,与抛物线相切于点P(-4,-4)的直线
的焦点,与抛物线相切于点P(-4,-4)的直线 轴的交点为Q,则
轴的交点为Q,则 。
。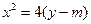 与圆
与圆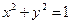 相交于第一象限的P点,且在P点处两曲线的切线互相垂直,则
相交于第一象限的P点,且在P点处两曲线的切线互相垂直,则 .
.