题目内容
已知函数f(x)=![]() 在[0,1]上的最小值为
在[0,1]上的最小值为![]() ,
,
(1)求f(x)的解析式; (2)证明:f(1)+f(2)+…+f(n)>n-![]() +
+![]() (n∈N
(n∈N![]() )
)
(1)f(x)=![]() ,(2)同解析。
,(2)同解析。
解析:
(1)∵a=0时f(x)=![]() 不合题意 ∴a≠0
不合题意 ∴a≠0
此时f(x)在[0,1]上是单调函数
又f(1)=![]() >
>![]() ∴f(x)为单调递增函数 ∴a<0
∴f(x)为单调递增函数 ∴a<0
由f(x)=![]() 即f(x)=
即f(x)=![]()
(2)∵f(n)= ![]() =1-
=1-![]()
>1-![]()
∴f(1)+f(2)+…+f(n) >1-![]()
=n-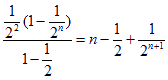

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
在(0,+∞)上单调递增,则实数k的取值范围是( )
| -k |
| x |
| A、(-∞,0) |
| B、(0,+∞) |
| C、(1,+∞) |
| D、(-∞,1) |
已知函数f(x)=
在区间[1,2]上的最大值为A,最小值为B,则A-B=( )
| 1 |
| x |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
 在x=0,x=
在x=0,x= 处存在极值。
处存在极值。
 ]上单调递增,则正实数
]上单调递增,则正实数