题目内容
某种奶粉每箱装6罐,其中有2罐不合格,质检人员从中随机抽出2罐,检测出不合格产品的概率为
- A.

- B.

- C.

- D.

C
分析:根据题意,设检测出不合格产品为事件A,易得A的对立事件为“没有检测出不合格产品”即抽出的2罐都合格,进而根据组合公式可得“从6罐中随机抽出2罐”和“抽出的2罐都合格”的情况数目,由等可能事件的概率公式计算可得P( ),由对立事件的概率性质,计算可得答案.
),由对立事件的概率性质,计算可得答案.
解答:设检测出不合格产品为事件A,“检测出不合格产品”的对立事件为“没有检测出不合格产品”即抽出的2罐都合格,
从6罐中随机抽出2罐,有C62=15种情况,
而抽出的2罐都合格即没有检测出不合格产品的有C42=6种情况,
即P( )=
)=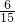 =
= ,则P(A)=1-
,则P(A)=1- =
= ;
;
故选C.
点评:本题考查等可能事件的概率计算,要利用相互对立的事件的概率之和为1来解题.
分析:根据题意,设检测出不合格产品为事件A,易得A的对立事件为“没有检测出不合格产品”即抽出的2罐都合格,进而根据组合公式可得“从6罐中随机抽出2罐”和“抽出的2罐都合格”的情况数目,由等可能事件的概率公式计算可得P(
 ),由对立事件的概率性质,计算可得答案.
),由对立事件的概率性质,计算可得答案.解答:设检测出不合格产品为事件A,“检测出不合格产品”的对立事件为“没有检测出不合格产品”即抽出的2罐都合格,
从6罐中随机抽出2罐,有C62=15种情况,
而抽出的2罐都合格即没有检测出不合格产品的有C42=6种情况,
即P(
 )=
)=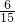 =
= ,则P(A)=1-
,则P(A)=1- =
= ;
;故选C.
点评:本题考查等可能事件的概率计算,要利用相互对立的事件的概率之和为1来解题.

练习册系列答案
相关题目











