题目内容
设n是正整数,如果1,2,3,…,2n的一个排列x1,x2,x3,…,x2n满足:在{1,2,…2n-1}中至少有一个i使得|xi-xi+1|=n,则称排列x1,x2,x3,…,x2n具有性质P.
(Ⅰ)当n=2时,写出4个具有性质P的排列;
(Ⅱ)求n=3时不具有性质P的排列的个数;
(Ⅲ)求证:对于任意n,具有性质P的排列比不具有性质P的排列多.
(Ⅰ)当n=2时,写出4个具有性质P的排列;
(Ⅱ)求n=3时不具有性质P的排列的个数;
(Ⅲ)求证:对于任意n,具有性质P的排列比不具有性质P的排列多.
分析:(I)根据x1,x2,x3,…,x2n具有性质P定义,可得n=2时,只要1,3或2,4相邻即可;
(II)当n=3时,1,2,3,4,5,6的全排列数为
; 1,4;2,5;3,6三对数中,至少有一对相邻的排列数为
;至少有两对相邻
;三对全相邻
,相减可得答案.
(III)记A={(x1,x2,x3,…,x2n)|(x1,x2,x3,…,x2n)具有性质P},B={(x1,x2,x3,…,x2n)|(x1,x2,x3,…,x2n)不具有性质P},C={(x1,x2,x3,…,x2n)|恰有某一个i使得|xi-xi+1|=n,i≠1},分析A中元素与B中元素个数的关系,可得答案.
(II)当n=3时,1,2,3,4,5,6的全排列数为
| A | 6 6 |
| C | 1 3 |
| A | 2 2 |
| A | 5 5 |
| C | 2 3 |
| A | 2 2 |
| 4 4 |
| A | 3 3 |
| A | 2 2 |
| 2 2 |
(III)记A={(x1,x2,x3,…,x2n)|(x1,x2,x3,…,x2n)具有性质P},B={(x1,x2,x3,…,x2n)|(x1,x2,x3,…,x2n)不具有性质P},C={(x1,x2,x3,…,x2n)|恰有某一个i使得|xi-xi+1|=n,i≠1},分析A中元素与B中元素个数的关系,可得答案.
解答:解:(I)当n=2时,具有性质P的排列有:
(2,1,3,4);(2,3,1,4);(4,1,3,2),(4,3,1,2)
(II)当n=3时,1,2,3,4,5,6的全排列数为
; 1,4;2,5;3,6三对数中,至少有一对相邻的排列数为
;至少有两对相邻
;三对全相邻
所以,n=3时不具有性质P的排列的个数共有:
-
-
-
=240;
证明:(III)记A={(x1,x2,x3,…,x2n)|(x1,x2,x3,…,x2n)具有性质P}
B={(x1,x2,x3,…,x2n)|(x1,x2,x3,…,x2n)不具有性质P}
C={(x1,x2,x3,…,x2n)|恰有某一个i使得|xi-xi+1|=n,i≠1}
显然C是A的子集,而且(n+1,1,2,…,n,n+2,…,2n)∈A,(n+1,1,2,…,n,n+2,…,2n)∉C,
所以C是A的真子集,所以A中元素个数大于C中元素个数;
考虑B中任一元素(y1,y2,y3,…,y2n),则|y2-y1|≠n,因此与y1相差n的数一定是某个yk,(k>2)
把y1放到yk的左边得到一个新排列(y2,y3,…,yk-1,y1,yk,…,y2n),这个排列一定是C的元素,
作映射(y1,y2,y3,…,y2n),→(y2,y3,…,yk-1,y1,yk,…,y2n),
不难证明这是一一对应,所以C中元素个数等于B中元素个数
综上A中元素个数大于B中元素个数
即对于任意n,具有性质P的排列比不具有性质P的排列多
(2,1,3,4);(2,3,1,4);(4,1,3,2),(4,3,1,2)
(II)当n=3时,1,2,3,4,5,6的全排列数为
| A | 6 6 |
| C | 1 3 |
| A | 2 2 |
| A | 5 5 |
| C | 2 3 |
| A | 2 2 |
| 4 4 |
| A | 3 3 |
| A | 2 2 |
| 2 2 |
所以,n=3时不具有性质P的排列的个数共有:
| A | 6 6 |
| C | 1 3 |
| A | 2 2 |
| A | 5 5 |
| C | 2 3 |
| A | 2 2 |
| 4 4 |
| A | 3 3 |
| A | 2 2 |
| 2 2 |
证明:(III)记A={(x1,x2,x3,…,x2n)|(x1,x2,x3,…,x2n)具有性质P}
B={(x1,x2,x3,…,x2n)|(x1,x2,x3,…,x2n)不具有性质P}
C={(x1,x2,x3,…,x2n)|恰有某一个i使得|xi-xi+1|=n,i≠1}
显然C是A的子集,而且(n+1,1,2,…,n,n+2,…,2n)∈A,(n+1,1,2,…,n,n+2,…,2n)∉C,
所以C是A的真子集,所以A中元素个数大于C中元素个数;
考虑B中任一元素(y1,y2,y3,…,y2n),则|y2-y1|≠n,因此与y1相差n的数一定是某个yk,(k>2)
把y1放到yk的左边得到一个新排列(y2,y3,…,yk-1,y1,yk,…,y2n),这个排列一定是C的元素,
作映射(y1,y2,y3,…,y2n),→(y2,y3,…,yk-1,y1,yk,…,y2n),
不难证明这是一一对应,所以C中元素个数等于B中元素个数
综上A中元素个数大于B中元素个数
即对于任意n,具有性质P的排列比不具有性质P的排列多
点评:本题考查的知识点是排列,组合,正确理解新定义x1,x2,x3,…,x2n具有性质P的含义,是解答的关键.

练习册系列答案
相关题目
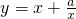 有如下性质:如果常数a>0,那么该函数在
有如下性质:如果常数a>0,那么该函数在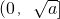 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.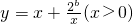 在(0,4]上是减函数,在[4,+∞)上是增函数,求b的值.
在(0,4]上是减函数,在[4,+∞)上是增函数,求b的值.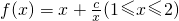 的最大值和最小值;
的最大值和最小值;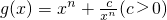 的单调性,并说明理由.
的单调性,并说明理由.