Question

【题目】如图，在四棱锥中，底面为直角梯形，，，平面底面，为的中点，是棱上的点，，，．

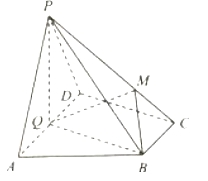
（1）求证：平面平面；

（2）若，求二面角的大小．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题分析：（1）借助题设条件运用面面垂直的判定定理推证；（2）借助题设运用空间向量的数量积公式求解．

试题解析：

（1）∵为的中点，，，

∴，，∴四边形是平行四边形，∴，

∵底面为直角梯形，，，∴．

又，∴平面．∵平面，∴平面平面．…………6分

（2）∵，平面底面，平面底面，

∴底面，

以为原点，为轴，为轴，为轴，建立空间直角坐标系，

则，，，，

设，则，

即，

∴，，，∴，

，，

设平面的法向量，则，

取，得，平面的法向量．

设二面角的平面角为，则，

∴，

∴二面角的大小为．………………12分