题目内容
(本小题满分8分)
已知函数f(x)=|x+1|+ax,(a∈R)
(1)若a=1,画出此时函数的图象.

|
【答案】
(1)f(x)=|x+1|+x=

(2)f(x)=
当a>1时,f(x)在[-1,+∞)单调递增,且f(x)≥f(-1)=-a,f(x)在(-∞,-1)单调递增,且f(x)<f(-1)=-a,因此f(x)在R上单调递增.
【解析】(1)根据零点分段法讨论去绝对值转化为分段函数.
(2)因为a>1,可知f(x)在[-1,+∞)和(-∞,-1)都是单调递增,确定在R上是否单调递增,关键是判断 时,f(x)≥f(-1)=-a;x>-1时,f(x)<f(-1)=-a.
时,f(x)≥f(-1)=-a;x>-1时,f(x)<f(-1)=-a.
(1)f(x)=|x+1|+x= ……………………………………2分
……………………………………2分

…………………………4分
(2)f(x)= ……………………………………6分
……………………………………6分
当a>1时,f(x)在[-1,+∞)单调递增,且f(x)≥f(-1)=-a,f(x)在(-∞,-1)单调递增,且f(x)<f(-1)=-a,因此f(x)在R上单调递增.…………………………8分

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 中,
中,
 ,证明:数列
,证明:数列 是等差数列;
是等差数列; 项和
项和 .
. ,
,
 .若
.若 ,求实数
,求实数 的取值范围.
的取值范围. 是首项为1,公比为2的等比数列,数列
是首项为1,公比为2的等比数列,数列 的前
的前 项和
项和 .
. 的前
的前
 ,
, ,当
,当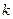 为何值时,
为何值时, 与
与 垂直?
垂直?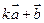 与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?