题目内容
(本小题满分8分)已知数列 是首项为1,公比为2的等比数列,数列
是首项为1,公比为2的等比数列,数列 的前
的前 项和
项和 .
.
(1)求数列 与
与 的通项公式;(2)求数列
的通项公式;(2)求数列 的前
的前 项和.
项和.
【答案】
(1) ,
, .(2)
.(2) .
.
【解析】本小题主要考查等差数列、等比数列等基础知识,考查运算求解能力和推理论证能力,求数列 与
与 的通项公式时分别用到等比数列的通项公式及
的通项公式时分别用到等比数列的通项公式及 的关系;数列
的关系;数列 是差比数列,求和时用错位相减法,分别列出
是差比数列,求和时用错位相减法,分别列出  ,
,
 ,
,
解:(1)因为数列 是首项为1,公比为2的等比数列,
是首项为1,公比为2的等比数列,
所以数列 的通项公式为
的通项公式为 .
.
因为数列 的前
的前 项和
项和 .
.
所以当 时,
时,
 ,
,
当 时,
时, ,
,
所以数列 的通项公式为
的通项公式为 .
.
(2)由(1)可知, .
.
设数列 的前
的前 项和为
项和为 ,
,
则
 ,
①
,
①
即  ,
②
,
②
①-②,得

 ,
,
所以 .
.
故数列 的前
的前 项和为
项和为 .
.

练习册系列答案
相关题目
 ,满足
,满足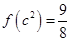
 的值;
的值;
 .
. ,集合A={
,集合A={ ,集合B=
,集合B=
 (2)
(2) 
 ,试确定
,试确定 的值,使得:
的值,使得: ;
(2)
;
(2) 
 ,
,  的夹角为
的夹角为 , 且
, 且 ,
,  ,
,  ; (2) 求
; (2) 求 .
.