题目内容
设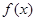 是连续的偶函数,且当
是连续的偶函数,且当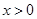 时
时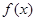 是单调函数,则满足
是单调函数,则满足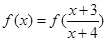 的所有
的所有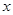 之和为( )
之和为( )
A.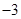 B.
B.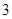 C.
C.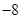 D.
D.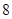
【答案】
C
【解析】
试题分析:根据已知函数 是连续的偶函数,且当
是连续的偶函数,且当 时
时 是单调函数,且有
是单调函数,且有 ,则说明而来
,则说明而来 ,那么解方程可知满足方程的解
,那么解方程可知满足方程的解 求解得到方程的根满足
求解得到方程的根满足 ,那么结合韦达定理可知四个根的和为-8,故选C.
,那么结合韦达定理可知四个根的和为-8,故选C.
考点:本试题考查了函数与方程的问题。
点评:对于方程根的求解,要结合函数的偶函数性质的对称性质,以及函数的单调性来分析得到结论,属于基础题。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
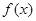 是连续的偶函数,且当
是连续的偶函数,且当 时,
时, 的所有
的所有 之和为( )
之和为( ) B.
B. C.5 D.
C.5 D.
 是连续的偶函数,且当
是连续的偶函数,且当 时,
时,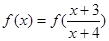 的所有
的所有 的和为 ( )
的和为 ( )