题目内容
在△ABC中,内角A,B,C所对边长分别为a,b,c,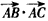 =8,∠BAC=θ,a=4,
=8,∠BAC=θ,a=4,
(Ⅰ)求b·c的最大值及θ的取值范围;
(Ⅱ)求函数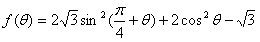 的最值。
的最值。
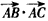 =8,∠BAC=θ,a=4,
=8,∠BAC=θ,a=4,(Ⅰ)求b·c的最大值及θ的取值范围;
(Ⅱ)求函数
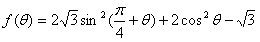 的最值。
的最值。解:(Ⅰ)bc·cosθ=8,b2+c2-2bccosθ=42,
即b2+c2=32,
又b2+c2≥2bc,
所以bc≤16,即bc的最大值为16,
即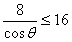 ,所以
,所以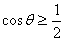 ,
,
又0<θ<π,所以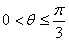 ;
;
(Ⅱ)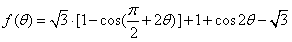
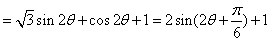 ,
,
因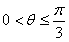 ,所以
,所以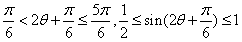 ,
,
当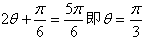 时,
时, ;
;
当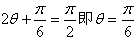 时,f(θ)max=2×1+1=3。
时,f(θ)max=2×1+1=3。
即b2+c2=32,
又b2+c2≥2bc,
所以bc≤16,即bc的最大值为16,
即
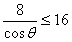 ,所以
,所以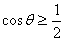 ,
,又0<θ<π,所以
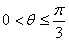 ;
;(Ⅱ)
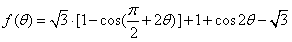
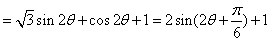 ,
,因
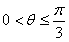 ,所以
,所以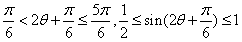 ,
,当
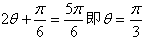 时,
时, ;
;当
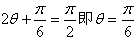 时,f(θ)max=2×1+1=3。
时,f(θ)max=2×1+1=3。
练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目