题目内容
8.已知a∈R,二次函数f(x)=ax2-2x-2a,设不等式f(x)>0的解集为A,又集合B={x|$\frac{3-x}{x-1}$>0},若A∩B=∅,求a的取值范围.分析 注意到△=4+8a2>0,则函数有两个零点,由a的正负,确定不等式解集的形式.结合着数轴分类讨论.
解答 .解:由题意可知二次函数a≠0,
令f(x)=0解得其两根为x1=$\frac{1+\sqrt{1+2{a}^{2}}}{a}$,x2=$\frac{1-\sqrt{1+2{a}^{2}}}{a}$,
(i)当a>0时,x1>0,x2<0,
A={x|x<x2}∪{x|x>x1},则A∩B=ϕ的充要条件是x1≥3,
即$\frac{1+\sqrt{1+2{a}^{2}}}{a}$≥3,
解得a∈(0,$\frac{6}{7}$]
(ii)当a<0时,x1<0,x2>0,A={x|x1<x<x2},
A∩B=ϕ的充要条件是x2≤1,
即$\frac{1-\sqrt{1+2{a}^{2}}}{a}$≤1,
解得a∈[-2,0)
综上,使A∩B=ϕ成立的a的取值范围为[-2,0)∪(0,$\frac{6}{7}$].
点评 在对集合的相关问题进行求解时,分类讨论时经常考查到的思想方法,另外对于一元二次不等式的解法也是一个基本的知识点,要熟练掌握

练习册系列答案
相关题目
16.已知命题p:?x∈[-1,2],函数f(x)=x2-x的值大于0,若p∨q是真命题,则命题q可以是( )
| A. | ?x∈(-1,1)使得cosx<$\frac{1}{2}$ | |
| B. | “-3<m<0”是“函数f(x)=x+log2x+m在区间($\frac{1}{2}$,2)上有零点”的必要不充分条件 | |
| C. | x=$\frac{π}{6}$是曲线f(x)=$\sqrt{3}$sin2x+cos2x的一条对称轴 | |
| D. | 若x∈(0,2),则在曲线f(x)=ex(x-2)上任意一点处的切线的斜率不小于-$\frac{1}{e}$ |
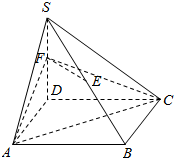 如图,四棱锥S-ABCD中,侧棱SD垂直于正方形ABCD所在的平面,E、F分别是SB、SD的中点,求证:
如图,四棱锥S-ABCD中,侧棱SD垂直于正方形ABCD所在的平面,E、F分别是SB、SD的中点,求证: