题目内容
在△ABC中，
分别为角
所对的边，若
，则△ABC的形状为( )
| A．钝角三角形 | B．直角三角形 | C．锐角三角形 | D．不能确定 |
A
解析试题分析：判定三角形内角是否为钝角，通常利用余弦定理，即根据角的余弦值的正负进行判断.因为
，所以
，因此△ABC的形状为钝角三角形.
考点：余弦定理
练习册系列答案
阅读快车系列答案
相关题目
如图所示，为了测量某湖泊两侧
间的距离，李宁同学首先选定了与不共线的一点
，然后给出了三种测量方案：（
的角
所对的边分别记为
）：
① 测量
② 测量
③测量
则一定能确定间距离的所有方案的序号为（ ）
| A．①② | B．②③ | C．①③ | D．①②③ |
在
中，角
的对边分别是
，且
，则
等于（ ）
A． | B． | C． | D． |
在锐角
中,角
对的边长分别为
.若
,则角
等于（ ）
A． | B． | C． | D． |
在△ABC中，
，
，△
的面积为
，则边
的值为()
A． | B． | C． | D． |
已知△ABC的周长为
，且
.若△ABC的面积为
,则角C的大小为（ ）
| A．30° | B．60° | C．90° | D．120° |
如图，设
两点在河的两岸，一测量者在
所在的同侧河岸边选定一点
，测出
的距离为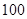
,
,
后，就可以计算出两点的距离为
A． m | B． m | C． m | D． m |
在锐角中△ABC，角A，B所对的边长分别为a,b.若2asinB=b
,则角A等于（ ）
A． | B． | C． | D． |
已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos 2A=0,a=7,c=6,则b等于( )
| A．10 | B．9 | C．8 | D．5 |